1. INTRODUCTION
Biological assays (also called bioassays) are an integral part of the quality assessment required for the manufacturing and marketing of many biological and some non-biological drug products. Bioassays commonly used for drug potency estimation can be distinguished from chemical tests by their reliance on a biological substrate (e.g., animals, living cells, or functional complexes of target receptors). Because of multiple operational and biological factors arising from this reliance on biology, they typically exhibit a greater variability than do chemically-based tests.
Bioassays are one of several physicochemical and biologic tests with procedures and acceptance criteria that control critical quality attributes of a biological drug product. As described in the ICH Guideline entitled Specifications: Test Procedures And Acceptance Criteria For Biotechnological/Biological Products (Q6B), section 2.1.2, bioassay techniques may measure an organism’s biological response to the product; a biochemical or physiological response at the cellular level; enzymatic reaction rates or biological responses induced by immunological interactions; or ligand- and receptor-binding. As new biological drug products and new technologies emerge, the scope of bioassay approaches is likely to expand. Therefore, general chapter Biological Assay Validation  1033
1033 emphasizes validation approaches that provide flexibility to adopt new bioassay methods, new biological drug products, or both in conjunction for the assessment of drug potency.
emphasizes validation approaches that provide flexibility to adopt new bioassay methods, new biological drug products, or both in conjunction for the assessment of drug potency.
Good manufacturing practice requires that test methods used for assessing compliance of pharmaceutical products with quality requirements should meet appropriate standards for accuracy and reliability. Assay validation is the process of demonstrating and documenting that the performance characteristics of the procedure and its underlying method meet the requirements for the intended application and that the assay is thereby suitable for its intended use. USP general chapter Validation of Compendial Procedures  1225
1225 and ICH Q2(R1) describe the assay performance characteristics (parameters) that should be evaluated for procedures supporting small-molecule pharmaceuticals. Although evaluation of these validation parameters is straightforward for many types of analytical procedures for well-characterized, chemically-based drug products, their interpretation and applicability for some types of bioassays has not been clearly delineated. This chapter addresses bioassay validation from the point of view of the measurement of activity rather than mass or other physicochemical measurements, with the purpose of aligning bioassay performance characteristics with uses of bioassays in practice.
and ICH Q2(R1) describe the assay performance characteristics (parameters) that should be evaluated for procedures supporting small-molecule pharmaceuticals. Although evaluation of these validation parameters is straightforward for many types of analytical procedures for well-characterized, chemically-based drug products, their interpretation and applicability for some types of bioassays has not been clearly delineated. This chapter addresses bioassay validation from the point of view of the measurement of activity rather than mass or other physicochemical measurements, with the purpose of aligning bioassay performance characteristics with uses of bioassays in practice.
Assessment of bioassay performance is a continuous process, but bioassay validation should be performed when development has been completed. Bioassay validation is guided by a validation protocol describing the goals and design of the validation study. General chapter  1033
1033 provides validation goals pertaining to relative potency bioassays. Relative potency bioassays are based on a comparison of bioassay responses for a Test sample to those of a designated Standard that provides a quantitative measure of the Test bioactivity relative to that of the Standard.
provides validation goals pertaining to relative potency bioassays. Relative potency bioassays are based on a comparison of bioassay responses for a Test sample to those of a designated Standard that provides a quantitative measure of the Test bioactivity relative to that of the Standard.
Validation parameters discussed include relative accuracy, specificity, intermediate precision, and range. Laboratories may use dilutional linearity to verify the relative accuracy and range of the method. Although robustness is not a requirement for validation, general chapter  1033
1033 recommends that a bioassay’s robustness be assessed prior to validation. In addition,
recommends that a bioassay’s robustness be assessed prior to validation. In addition,  1033
1033 describes approaches for validation design (sample selection and replication strategy), validation acceptance criteria, data analysis and interpretation, and finally bioassay performance monitoring through quality control. Documentation of bioassay validation results is also discussed, with reference to pre-validation experiments performed to optimize bioassay performance. In the remainder of general chapter
describes approaches for validation design (sample selection and replication strategy), validation acceptance criteria, data analysis and interpretation, and finally bioassay performance monitoring through quality control. Documentation of bioassay validation results is also discussed, with reference to pre-validation experiments performed to optimize bioassay performance. In the remainder of general chapter  1033
1033 the term “bioassay” should be interpreted as meaning “relative potency bioassay”.
the term “bioassay” should be interpreted as meaning “relative potency bioassay”.
2. FUNDAMENTALS OF BIOASSAY VALIDATION
The goal of bioassay validation is to confirm that the operating characteristics of the procedure are such that the procedure is suitable for its intended use. The issues involved in developing a bioassay are described in greater detail in general chapter  1032
1032 and are assumed resolved by the time the bioassay is in validation. Included in those decisions will be identification of what constitutes an assay and a run for the bioassay. Multiple dilutions (concentrations) of the Standard and one or more Test samples constitute a replicate set (also known as a minimal set), which contain a test substrate (e.g., group of animals or vessel of cells) at each dilution for each sample [Test(s) and Standard]. A run is defined as work performed during a period when the accuracy (trueness) and precision in the assay system can reasonably be expected to be stable. In practice, a run frequently consists of the work performed by a single analyst in one lab, with one set of equipment, in a short period of time (typically a day). An assay is the body of data used to assess similarity and estimate potency relative to a Standard for each Test sample in the assay. A run may contain multiple assays, a single assay, or part of an assay. Multiple assays may be combined to yield a reportable value for a sample. The reportable value is the value that is compared to a product specification.
and are assumed resolved by the time the bioassay is in validation. Included in those decisions will be identification of what constitutes an assay and a run for the bioassay. Multiple dilutions (concentrations) of the Standard and one or more Test samples constitute a replicate set (also known as a minimal set), which contain a test substrate (e.g., group of animals or vessel of cells) at each dilution for each sample [Test(s) and Standard]. A run is defined as work performed during a period when the accuracy (trueness) and precision in the assay system can reasonably be expected to be stable. In practice, a run frequently consists of the work performed by a single analyst in one lab, with one set of equipment, in a short period of time (typically a day). An assay is the body of data used to assess similarity and estimate potency relative to a Standard for each Test sample in the assay. A run may contain multiple assays, a single assay, or part of an assay. Multiple assays may be combined to yield a reportable value for a sample. The reportable value is the value that is compared to a product specification.
In assays that involve groups at each dilution (e.g., 6 samples, each at 10 dilutions, in the non-edge wells of each of several 96-well cell culture plates) the groups (plates) constitute statistical blocks that should be elements in the assay and validation analyses (blocks are discussed in  1032
1032 ). Within-block replicates for Test samples are rarely cost-effective. Blocks will not be further discussed in this chapter; more detailed discussion is found in
). Within-block replicates for Test samples are rarely cost-effective. Blocks will not be further discussed in this chapter; more detailed discussion is found in  1032
1032 .
.
The amount of activity (potency) of the Standard is initially assigned a value of 1.0 or 100%, and the potency of the Test sample is calculated by comparing the concentration–response curves for the Test and Standard pair. This results in a unitless measure, which is the relative potency of the Test sample in reference to the potency of the Standard. In some cases the Standard is assigned a value according to another property such as protein concentration. In that case the potency of the Test sample is the relative potency times the assigned value of the Standard. An assumption of parallel-line or parallel-curve (e.g., four-parameter logistic) bioassays is that the dose–response curves that are generated using a Standard and a Test sample have similar (parallel) curve shape distinguished only by a horizontal shift in the log dose. For slope-ratio bioassays, curves generated for Standard and Test samples should be linear, pass through a common intercept, and differ only by their slopes. Information about how to assess parallelism is provided in general chapters  1032
1032 and
and  1034
1034 .
.
In order to establish the relative accuracy and range of the bioassay, validation Test samples may be constructed using a dilution series of the Standard to assess dilutional linearity (linearity of the relationship between known and measured relative potency). In addition, the validation study should yield a representative estimate of the variability of the relative potency determination. Although robustness studies are usually performed during bioassay development, key factors in these studies such as incubation time and temperature and, for cell-based bioassays, cell passage number and cell number may be included in the validation, particularly if they interact with another factor that is introduced during the validation (e.g., a temperature sensitive reagent that varies in its sensitivity from lot-to-lot). Because of potential influences on the bioassay from inter-run factors such as multiple analysts, instruments, or reagent sources, the design of the bioassay validation should include consideration of these factors. The variability of potency from these combined elements defines the intermediate precision (IP) of the bioassay. An appropriate study of the variability of the potency values obtained, including the impact of intra-assay and inter-run factors, can help the laboratory confirm an adequate testing strategy and forecast the inherent variability of the reportable value (which may be the average of multiple potency determinations). Variability estimates can also be utilized to establish the sizes of differences (fold difference) that can be distinguished between samples tested in the bioassay. (See section 3.4 Use of Validation Results for Bioassay Characterization.)
Demonstrating specificity (also known as selectivity) requires evidence of lack of influence from matrix components such as manufacturing process components or degradation products so that measurements quantify the target molecule only. Other analytical methods may complement a bioassay in measuring or identifying other components in a sample.
2.1 Bioassay Validation Protocol
A bioassay validation protocol should include the number and types of samples that will be studied in the validation; the study design, including inter-run and intra-run factors; the replication strategy; the intended validation parameters and justified target acceptance criteria for each parameter; and a proposed data-analysis plan. Note that in regard to satisfying acceptance criteria, failure to find a statistically significant effect is not an appropriate basis for defining acceptable performance in a bioassay; conformance to acceptance criteria may be better evaluated using an equivalence approach.
In addition, assay, run, and sample acceptance criteria such as system suitability and similarity should be specified before performing the validation. Depending on the extent of development of the bioassay, these may be proposed as tentative and can be updated with data from the validation. Assay, run, or sample failures may be reassessed according to criteria which have been defined in the validation protocol and, with sound justification, included in the overall validation assessment. Additional validation trials may be required in order to support changes to the method.
The bioassay validation protocol should include target acceptance criteria for the proposed validation parameters. Steps to be taken upon failure to meet a target acceptance criterion should be specified in the validation protocol, and may result in a limit on the range of potencies that can be measured in the bioassay or a modification to the replication strategy in the bioassay procedure.
2.2 Documentation of Bioassay Validation Results
Bioassay validation results should be documented in a bioassay validation report. The validation report should support the conclusion that the method is fit for use or should indicate corrective action (such as an increase in the replication strategy) that will be undertaken to generate sufficiently reliable results to achieve fitness for use. The report could include the raw data and intermediate results (e.g., variance component estimates should be provided in addition to overall intermediate precision) which would facilitate reproduction of the bioassay validation analysis by an independent reviewer. Estimates of validation parameters should be reported at each level and overall as appropriate. Deviations from the validation protocol should be documented with justification. The conclusions from the study should be clearly described with references to follow-up action as necessary. Follow-up action can include amendment of system or sample suitability criteria or modification of the bioassay replication strategy. Reference to prevalidation experiments may be included as part of the validation study report. Prevalidation experiments may include robustness experiments, where bioassay parameters have been identified and ranges have been established for significant parameters, and also may include qualification experiments, where the final procedure has been performed to confirm satisfactory performance in routine operation. Conclusions from prevalidation and qualification experiments performed during development contribute to the description of the operating characteristics of the bioassay procedure.
2.3 Bioassay Validation Design
The biological assay validation should include samples that are representative of materials that will be tested in the bioassay and should effectively establish the performance characteristics of the procedure. For relative accuracy, sample relative potency levels that bracket the range of potencies that may be tested in the bioassay should be used. Thus samples that span a wide range of potencies might be studied for a drug or biological with a wide specification range or for a product that is inherently unstable, but a narrower range can be used for a more durable product. A minimum of three potency levels is required, and five are recommended for a reliable assessment. If the validation criteria for relative accuracy and IP are satisfied, the potency levels chosen will constitute the range of the bioassay. A limited range will result from levels that fail to meet their target acceptance criteria. Samples may also be generated for the bioassay validation by stressing a sample to a level that might be observed in routine practice (i.e., stability investigations). Additionally, the influences of the sample matrix (excipients, process constituents, or combination components) can be studied strategically by intentionally varying these together with the target analyte, using a multifactorial approach. Often this will have been done during development, prior to generating release and stability data.
The bioassay validation design should consider all facets of the measurement process. Sources of bioassay measurement variability include sample preparation, intra-run factors, and inter-run factors. Representative estimation of bioassay variability necessitates consideration of these factors. Test sample and Standard preparation should be performed independently during each validation run.
The replication strategy used in the validation should reflect knowledge of the factors that might influence the measurement of potency. Intra-run variability may be affected by bioassay operating factors that are usually set during development (temperature, pH, incubation times, etc.); by the bioassay design (number of animals, number of dilutions, replicates per dilution, dilution spacing, etc.); by the assay acceptance and sample acceptance criteria; and by the statistical analysis (where the primary endpoints are the similarity assessment for each sample and potency estimates for the reference samples). Operating restrictions and bioassay design (intra- and inter-run formulae that result in a reportable value for a test material) are usually specified during development and may become a part of the bioassay operating procedure. IP is studied by independent runs of the procedure, perhaps using an experimental design that alters those factors that may have an impact on the performance of the procedure. Experiments (including those that implement formalized design of experiments [DOE]) with nested or crossed design structure can reveal important sources of variability in the procedure, as well as ensure a representative estimate of long-term variability. During the validation it is not necessary to employ the format required to achieve the reportable value for a Test sample. A well-designed validation experiment that combines both intra-run and inter-run sources of variability provides estimates of independent components of the bioassay variability. These components can be used to verify or forecast the variability of the bioassay format.
A thorough analysis of the validation data should include graphical and statistical summaries of the validation parameters’ results and their conformance to target acceptance criteria. The analysis should follow the specifics of the data-analysis plan outlined in the validation protocol. In most cases, log relative potency should be analyzed in order to satisfy the assumptions of the statistical methods (see section 2.7 Statistical Considerations, Scale of Analysis,). Those assumptions include normality of the distribution from which the data were sampled and homogeneity of variability across the range of results observed in the validation. These assumptions can be explored using graphical techniques such as box plots and probability plots. The assumption of normality can be investigated using statistical tests of normality across a suitably sized collection of historical results. Alternative methods of analysis should be sought when the assumptions can be challenged. Confidence intervals should be calculated for the validation parameters, using methods described here and in general chapter Analytical Data—Interpretation and Treatment  1010
1010 .
.
2.4 Validation Strategies for Bioassay Performance Characteristics
Parameters that should be verified in a bioassay are relative accuracy, specificity, IP (which incorporates repeatability), and range. Other parameters discussed in general chapter  1225
1225 and ICH Q2(R1) such as detection limit and quantitation limit have not been included because they are usually not relevant to a bioassay that reports relative potency. These may be relevant, however, to the validation of an ancillary assay such as one used to score responders or measure response in conjunction with an in vivo potency assay. Likewise linearity is not part of bioassay validation, except as it relates to relative accuracy (dilutional linearity). There follow strategies for addressing bioassay validation parameters.
and ICH Q2(R1) such as detection limit and quantitation limit have not been included because they are usually not relevant to a bioassay that reports relative potency. These may be relevant, however, to the validation of an ancillary assay such as one used to score responders or measure response in conjunction with an in vivo potency assay. Likewise linearity is not part of bioassay validation, except as it relates to relative accuracy (dilutional linearity). There follow strategies for addressing bioassay validation parameters.
Relative Accuracy—
The relative accuracy of a relative potency bioassay is the relationship between measured relative potency and known relative potency. Relative accuracy in bioassay refers to a unit slope (slope = 1) between log measured relative potency and log known relative potency. The most common approach to demonstrating relative accuracy for relative potency bioassays is by construction of target potencies by dilution of the standard material or a Test sample with known potency. This type of study is often referred to as a dilutional linearity study. The results from a dilutional linearity study should be assessed using the estimated relative bias at individual levels and via a trend in relative bias across levels. The relative bias at individual levels is calculated as follows:
The trend in bias is measured by the estimated slope of log measured potency versus log target potency, which should be held to a target acceptance criterion. If there is no trend in relative bias across levels, the estimated relative bias at each level can be held to a prespecified target acceptance criterion that has been defined in the validation protocol (see section 3 A Bioassay Validation Example).
Specificity—
For products or intermediates associated with complex matrices, specificity involves demonstrating lack of interference from matrix components or product-related components that can be expected to be present. This can be assessed via parallel dilution of the Standard with and without a spike addition of the potentially interfering compound. If the curves are similar and the potency conforms to expectations of a Standard-to-Standard comparison, the bioassay is specific against the compound. For these assessments both similarity and potency may be assessed using appropriate equivalence tests.
Specificity may also refer to the capacity of the bioassay to distinguish between different but related biopharmaceutical molecules. An understanding should be sought of the molecule and any related forms, and of opportunities for related molecules to be introduced into the bioassay.
Intermediate Precision—
Because of potential influences on the bioassay by factors such as analysts, instruments, or reagent lots, the design of the bioassay validation should include evaluation of these factors. The overall variability from measurements taken under a variety of normal test conditions within one laboratory defines the IP of the bioassay. IP is the ICH and USP term for what is also commonly referred to as inter-run variability. IP measures the influence of factors that will vary over time after the bioassay is implemented. These influences are generally unavoidable and include factors like change in personnel (new analysts), receipt of new reagent lots, etc.
When the validation has been planned using multifactor DOE, the impact of each factor can first be explored graphically to establish important contributions to potency variability. The identification of important factors should lead to procedures that seek to control their effects, such as further restrictions on intra-assay operating conditions or strategic qualification procedures on inter-run factors such as analysts, instruments, and reagent lots.
Contributions of validation study factors to the overall IP of the bioassay can be determined by performing a variance component analysis on the validation results. Variance component analysis is best carried out using a statistical software package that is capable of performing a mixed-model analysis with restricted maximum likelihood estimation (REML).
A variance component analysis yields variance component estimates such as
and
corresponding to intra-run and inter-run variation. These can be used to estimate the IP of the bioassay, as well as the variability of the reportable value for different bioassay formats (format variability). IP expressed as percent geometric coefficient of variation (%GCV) is given by the following formula, in this case using the natural log of the relative potency in the analysis (see section 2.7 Statistical Considerations, Scale of Analysis):
The variability of the reportable value from testing performed with n replicate sets in each of k runs (format variability) is equal to:
This formula can be used to determine a testing format suitable for various uses of the bioassay (e.g., release testing and stability evaluation).
Range—
The range of the bioassay is defined as the true or known potencies for which it has been demonstrated that the analytical procedure has a suitable level of relative accuracy and IP. The range is normally derived from the dilutional linearity study and minimally should cover the product specification range for potency. For stability testing and to minimize having to dilute or concentrate hyper- or hypo-potent Test samples into the bioassay range, there is value in validating the bioassay over a broader range.
2.5 Validation Target Acceptance Criteria
The validation target acceptance criteria should be chosen to minimize the risks inherent in making decisions from bioassay measurements and to be reasonable in terms of the capability of the art. When there is an existing product specification, acceptance criteria can be justified on the basis of the risk that measurements may fall outside of the product specification. Considerations from a process capability (Cp) index can be used to inform bounds on the relative bias (RB) and the IP of the bioassay. This chapter uses the following Cpm index:
where USL and LSL are the upper and lower release specification, RB is a bound on the degree of relative bias in the bioassay, and
and
are target product variance (i.e., lot-to-lot variability) and release assay variance (with associated format) respectively. (See section 3 A Bioassay Validation Example for an example of determination of
and Cpm.) This formulation requires prior knowledge regarding target product variability, or the inclusion of a random selection of lots to estimate this characteristic as part of the validation. Given limited understanding of assay performance, manufacturing history, and final specifications during development, this approach may be used simply as a guide for defining validation acceptance criteria.
The choice of a bound on Cpm is a business decision. The proportion of lots that are predicted to be outside their specification limits is a function of Cpm. Some laboratories require process capability corresponding to Cpm greater than or equal to 1.3. This corresponds to approximately a 1 in 10,000 chance that a lot with potency at the center of the specification range will be outside the specification limits.
When specifications have yet to be established for a product, a restriction on relative bias or IP can be formulated on the basis of the capability of the art of the bioassay methodology. For example, although chemical assays and immunoassays are often capable of achieving near single digit percent coefficient of variation (%CV, or percent relative standard deviation, %RSD), a more liberal restriction might be placed on bioassays, such as animal potency bioassays, that operate with much larger variability (measured as %GCV which can be compared to %CV; see Appendix). In this case the validation goal might be to characterize the method, using the validation results to establish an assay format that is predicted to yield reliable product measurements. A sound justification for target acceptance criteria or use of characterization should be included in the validation protocol.
2.6 Assay Maintenance
Once a bioassay has been validated it can be implemented. However, it is important to monitor its behavior over time. This is most easily accomplished by maintaining statistical process control (SPC) charts for suitable parameters of the Standard response curve and potency of assay QC samples. The purpose of these charts is to identify at an early stage any shift or drift in the bioassay. If a trend is observed in any SPC chart, the reason for the trend should be identified. If the resolution requires a modification to the bioassay or if a serious modification of the bioassay has occurred for other reasons (for example, a major technology change), the modified bioassay should be revalidated or linked to the original bioassay by an adequately designed bridging study with acceptance criteria that use equivalence testing.
2.7 Statistical Considerations
Several statistical considerations are associated with designing a bioassay validation and analyzing the data. These relate to the properties of bioassay measurements as well as the statistical tools that can be used to summarize and interpret bioassay validation results.
Scale of Analysis—
The scale of analysis of bioassay validation, where data are the relative potencies of samples in the validation study, must be considered in order to obtain reliable conclusions from the study. This chapter assumes that appropriate methods are already in place to reduce the raw bioassay response data to relative potency (as described in general chapter  1034
1034 ). Relative potency measurements are typically nearly log normally distributed. Log normally distributed measurements are skewed and are characterized by heterogeneity of variability, where the standard deviation is proportional to the level of response. The statistical methods outlined in this chapter require that the data be symmetric, approximating a normal distribution, but some of the procedures require homogeneity of variability in measurements across the potency range. Typically, analysis of potency after log transformation generates data that more closely fulfill both of these requirements. The base of the log transformation does not matter as long as a consistent base is maintained throughout the analysis. Thus, for example, if the natural log (log to the base e) is used to transform relative potency measurements, summary results are converted back to the bioassay scale utilizing base e.
). Relative potency measurements are typically nearly log normally distributed. Log normally distributed measurements are skewed and are characterized by heterogeneity of variability, where the standard deviation is proportional to the level of response. The statistical methods outlined in this chapter require that the data be symmetric, approximating a normal distribution, but some of the procedures require homogeneity of variability in measurements across the potency range. Typically, analysis of potency after log transformation generates data that more closely fulfill both of these requirements. The base of the log transformation does not matter as long as a consistent base is maintained throughout the analysis. Thus, for example, if the natural log (log to the base e) is used to transform relative potency measurements, summary results are converted back to the bioassay scale utilizing base e.
The distribution of potency measurements should be assessed as part of bioassay development (as described in  1032
1032 ). If it is determined that potency measurements are normally distributed, the validation can be carried out using methods described in the general chapter Validation of Compendial Procedures
). If it is determined that potency measurements are normally distributed, the validation can be carried out using methods described in the general chapter Validation of Compendial Procedures  1225
1225 .
.
As a consequence of the usual (for parallel-line assays) log transformation of relative potency measurements, there are advantages if the levels selected for the validation study are evenly spaced on the log scale. An example with five levels would be 0.50, 0.71, 1.00, 1.41, and 2.00. Intermediate levels are obtained as the geometric mean of two adjacent levels. Thus for example, the mid-level between 0.50 and 1.0 is derived as follows:
Likewise, summary measures of the validation are influenced by the log normal scale. Predicted response should be reported as the geometric mean of individual relative potency measurements, and variability expressed as %GCV. GCV is calculated as the anti-log of the standard deviation, Slog, of log transformed relative potency measurements. The formula is given by:
GCV = antilog(Slog)  1
1
Variability is expressed as GCV rather than RSD of the log normal distribution in order to preserve continuity using the log transformation (see additional discussion in the Appendix to this chapter). Intervals that might be calculated from GCV will be consistent with intervals calculated from mean and standard deviation of log transformed data. Table 1 presents an example of the calculation of geometric mean (GM) and associated RB, with %GCV for a series of relative potency measurements performed on samples tested at the 1.00 level. The log base e is used in the illustration.
Table 1. Illustration of calculations of GM and %GCV
| RP1 | In RP | |
|---|---|---|
| 1.1299 | 0.1221 | |
| 0.9261 | ||
| 1.1299 | 0.1221 | |
| 1.0143 | 0.0142 | |
| 1.0027 | 0.0027 | |
| 1.0316 | 0.0311 | |
| 1.1321 | 0.1241 | |
| 1.0499 | 0.0487 | |
| Average | 0.0485 | GM = 1.0497 |
| RB = 4.97% | ||
| SD | 0.0715 | %GCV = 7.4% |
|
1
Relative potency (RP) is the geometric mean of duplicate potencies measured in the eight runs of the example given in Table 4.
|
||
Here the GM of the relative potency measurements is calculated as the anti-log of the average log relative potency measurements and then expressed as relative bias, the percent deviation from the target potency:
GM = eAverage = e0.0485 = 1.0497
and the percent geometric coefficient of variation (%GCV) is calculated as:
%GCV = 100·(eSD  1)% = 100· (e0.0715
1)% = 100· (e0.0715  1)% = 7.4%
1)% = 7.4%
Note that the %GCV calculated for this illustration is not equal to the IP determined in the bioassay validation example for the 1.00 level (8.5%); see Table 6. This illustration utilizes the average of within-run replicates, while the IP in the validation example represents the variability of individual replicates.
Reporting Validation Results Using Confidence Intervals—
Estimates of bioassay validation parameters should be presented as a point estimate together with a confidence interval. A point estimate is the numerical value obtained for the parameter, such as the GM or %GCV. A confidence interval’s most common interpretation is as the likely range of the true value of the parameter. The previous example determines a 90% confidence interval for average log relative potency, CIln, as follows:
For percent relative bias this is:
The statistical constant (1.89) is from a t-table, with degrees of freedom (df) equal to the number of measurements minus one (df = 8  1 = 7). A confidence interval for IP or format variability can be formulated using methods for variance components; these methods are not covered in this general chapter.
1 = 7). A confidence interval for IP or format variability can be formulated using methods for variance components; these methods are not covered in this general chapter.
Assessing Conformance to Acceptance Criteria—
Bioassay validation results are compared to target acceptance criteria in order to demonstrate that the bioassay is fit for use. The process of establishing conformance of validation parameters to validation acceptance criteria should not be confused with establishing conformance of relative potency measurements to product specifications. Product specifications should inform the process of setting validation acceptance criteria.
A common practice is to apply acceptance criteria to the estimated validation parameter. This does not account, however, for the uncertainty in the estimated validation parameter. A solution is to hold the confidence interval on the validation parameter to the acceptance criterion. This is a standard statistical approach used to demonstrate conformance to expectation and is called an equivalence test. It should not be confused with the practice of performing a significance test, such as a t-test, which seeks to establish a difference from some target value (e.g., 0% relative bias). A significance test associated with a P-value > 0.05 (equivalent to a confidence interval that includes the target value for the parameter) indicates that there is insufficient evidence to conclude that the parameter is different from the target value. This is not the same as concluding that the parameter conforms to its target value. The study design may have too few replicates, or the validation data may be too variable to discover a meaningful difference from target. Additionally, a significance test may detect a small deviation from target that is of negligible importance. These scenarios are illustrated in Figure 1.
Figure 1. Use of confidence intervals to establish that validation results conform to an acceptance criterion.
The solid horizontal line represents the target value (perhaps 0% relative bias), and the dashed lines form the lower (LAL) and upper (UAL) acceptance limits. In scenario a, the confidence bound includes the target, and thus one could conclude there is insufficient evidence to conclude a difference from target (the significance test approach). However, although the point estimate (the solid diamond) falls within the acceptance range, the interval extends outside the range, which signifies that the true relative bias may be outside the acceptable range. In scenario b, the interval falls within the acceptance range, signifying conformance to the acceptance criterion. The interval in scenario c also falls within the acceptance range but excludes the target. Thus, for scenario c, although the difference of the point estimate from the target is statistically significant, c is acceptable because the confidence interval falls within the target acceptance limits.
Using the 90% confidence interval calculated previously, we can establish whether the bioassay has acceptable relative bias at the 1.00 level compared to a target acceptance criterion of no greater than +12%, for example. Because the 90% confidence interval for percent relative bias (0.07%, 10.1%) falls within the interval (100*[(1/1.12)  1]%, 100*[(1.12/1)
1]%, 100*[(1.12/1)  1]%) = (
1]%) = ( 11%, 12%), we conclude that there is acceptable relative bias at the 1.00 level. Note that a 90% confidence interval is used in an equivalence test rather than a conventional 95% confidence interval. This is common practice and is the same as the two one-sided tests (TOST) approach used in pharmaceutical bioequivalence testing.
11%, 12%), we conclude that there is acceptable relative bias at the 1.00 level. Note that a 90% confidence interval is used in an equivalence test rather than a conventional 95% confidence interval. This is common practice and is the same as the two one-sided tests (TOST) approach used in pharmaceutical bioequivalence testing.
Risks in Decision-Making and Number of Validation Runs—
The application of statistical tests, including the assessment of conformance of a validation parameter to its acceptance criteria, involves risks. One risk is that the parameter does not meet its acceptance criterion although the property associated with that parameter is satisfactory; another, the converse, is that the parameter meets its acceptance criterion although the parameter is truly unsatisfactory. A consideration related to these risks is sample size.
The two types of risk can be simultaneously controlled via strategic design, including choice of the number of runs that will be conducted in the validation. Specifically, the minimum number of runs needed to establish conformance to an acceptance criterion for relative bias is given by:
where t ,df and t
,df and t ,df are distributional points from a Student’s t-distribution;
,df are distributional points from a Student’s t-distribution;  and
and  are the one-sided type I and type II errors, and represent the risks associated with drawing the wrong conclusion in the validation; df is the degrees of freedom associated with the study design (usually n
are the one-sided type I and type II errors, and represent the risks associated with drawing the wrong conclusion in the validation; df is the degrees of freedom associated with the study design (usually n  1);
1);
is a preliminary estimate of IP; and 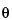 is the acceptable deviation (target acceptance criterion).
is the acceptable deviation (target acceptance criterion).
For example, if the acceptance criterion for relative bias is ± 0.11 log (i.e., 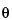 = 0.11), the bioassay variability is
= 0.11), the bioassay variability is
and  =
=  = 0.05,
= 0.05,
Note that this formulation of sample size assumes no intrinsic bias in the bioassay. A more conservative solution includes some nonzero bias in the determination of a sample size. This results in a greater sample size to offset the impact of the bias on the conclusions of the validation. In the current example the sample size increases to 10 runs if one assumes an intrinsic bias equal to 2%. Note also that this calculation represents a recursive solution (because the degrees of freedom depend on n) requiring statistical software or an algorithm that employs iterative methodology.
Note further that the selection of  and
and  should be justified on the basis of the corresponding risks of drawing the wrong conclusion from the validation.
should be justified on the basis of the corresponding risks of drawing the wrong conclusion from the validation.
Modeling Validation Results Using Mixed Effects Models—
Many analyses associated with bioassay validation must account for multiple design factors such as fixed effects (e.g., potency level), as well as random effects (e.g., analyst, run, and replicate). Statistical models composed of both fixed and random effects are called mixed effects models and usually require sophisticated statistical software for analysis. The results of the analysis may be summarized in an analysis of variance (ANOVA) table or a table of variance component estimates. The primary goal of the analysis is to estimate critical parameters rather than establish the significance of an effect. The modeling output provides parameter estimates together with their standard errors of estimates that can be utilized to establish conformance of a validation parameter to its acceptance criterion. Thus the average relative bias at each level is obtained as a portion of the analysis together with its associated variability. These compose a confidence interval that is compared to the acceptance criterion as described above. If variances across levels can be pooled, statistical modeling can also determine the overall relative bias and IP by combining information across levels performed in the validation. Similarly, mixed effects models can be used to obtain variance components for validation study factors and to combine results across validation study samples and levels.
Statistical Design—
Statistical designs, such as multifactor DOE or nesting, can be used to organize assay and runs in a bioassay validation. It is useful to incorporate factors that are believed to influence the bioassay response and that vary during long-term use of the procedure into these designs. Using these methods of design, the sources of variability may be characterized and a strategic test plan to manage the variability of the bioassay may be developed.
Table 2 shows an example of a multifactor DOE that incorporates multiple analysts, multiple cell culture preparations, and multiple reagent lots into the validation plan.
Table 2. Example of a Multifactor DOE with 3 Factors
| Run | Analyst | Cell Prep | Reagent Lot |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 2 |
| 3 | 1 | 2 | 1 |
| 4 | 1 | 2 | 2 |
| 5 | 2 | 1 | 1 |
| 6 | 2 | 1 | 2 |
| 7 | 2 | 2 | 1 |
| 8 | 2 | 2 | 2 |
In this design each analyst performs the bioassay with both cell preparations and both reagent lots. This is an example of a full factorial design because all combinations of the factors are performed in the validation study. To reduce the number of runs in the study, fractional factorial designs may be employed when more than three factors have been identified. For example, if it is practical for an analyst to perform four assays in a run, a split-unit design could be used with analysts as the whole-plot factor and cell preparation and reagent lot as sub-plot factors. Unlike screening experiments, the validation design should incorporate as many factors at as many levels as possible in order to obtain a representative estimate of IP. More than two levels of a factor should be employed in the design whenever possible. This may be accomplished in a less structured manner, without regard to strict factorial layout. Validation runs should be randomized whenever possible to mitigate the potential influences of run order or time.
Figure 2 illustrates an example of a validation using nesting (replicates nested within plate, plate nested within analyst).
For both of these types of design as well as combinations of the two, components of variability can be estimated from the validation results. These components of variability can be used to identify significant sources of variability as well as to derive a bioassay format that meets the procedure’s requirements for precision. It should be noted that significant sources of variability may have been identified during bioassay development. In this case the validation should confirm both the impact of these factors and the assay format that meets the requirement for precision.
Significant Figures—
The number of significant figures in a reported result from a bioassay is related to the latter’s precision. In general, a bioassay with %GCV between 2% and 20% will support two significant figures. The number of significant figures should not be confused with the number of decimal places—reported values equal to 1.2 and 0.12 have the same number (two) of significant figures. This standard of rounding is appropriate for log scaled measurements that have constant variation on the log scale and proportional rather than additive variability on the original scale (or the scale commonly used for interpretation). Note that rounding occurs at the end of a series of calculations when the final measurement is reported and used for decision making such as conformance to specifications. Thus if the final measurement is a reportable value from multiple assays, rounding should not occur prior to determination of the reportable value. Likewise, specifications should be stated with the appropriate number of significant figures.
3. A BIOASSAY VALIDATION EXAMPLE
An example illustrates the principles described in this chapter. The bioassay will be used to support a specification range of 0.71 to 1.41 for the product. Using the Cpm described in section 2.5 Validation Target Acceptance Criteria, a table is derived showing the projected rate of OOS results for various restrictions on RB and IP. Cpm is calculated on the basis of the variability of a reportable value using three independent runs of the bioassay (see discussion of format variability, above). Product variability is assumed to be equal to 0 in the calculations. The laboratory may wish to include target product variability. An estimate of target product variability can be obtained from data from a product, for example, manufactured by a similar process.
Table 3. Cpm and Probability of OOS for Various Restrictions on RB and IP
| LSL-USL | IP (%) | RB (%) | Cpm | Prob(OOS) (%) |
|---|---|---|---|---|
| 0.71–1.41 | 20 | 20 | 0.54 | 10.5 |
| 0.71–1.41 | 8 | 12 | 0.94 | 0.48 |
| 0.71–1.41 | 10 | 5 | 1.55 | 0.0003 |
The calculation is illustrated for IP equal to 8% and relative bias equal to 12% (n = 3 runs):
Prob(OOS) = 2·F( 3·0.94) = 0.0048 (0.48%),
3·0.94) = 0.0048 (0.48%),
where F represents the standard normal cumulative distribution function.
From Table 3, acceptable performance (less than 1% chance of obtaining an OOS result due to bias and variability of the bioassay) can be expected if the IP is  8% and relative bias is
8% and relative bias is  12%. The sample size formula given in section 2.7 Statistical Considerations, Risks in Decision-Making and Number of Validation Runs can be used to derive the number of runs required to establish conformance to an acceptance criterion for relative bias equal to 12% (using %GCVIP = 8%;
12%. The sample size formula given in section 2.7 Statistical Considerations, Risks in Decision-Making and Number of Validation Runs can be used to derive the number of runs required to establish conformance to an acceptance criterion for relative bias equal to 12% (using %GCVIP = 8%;  =
=  = 0.05):
= 0.05):
Thus eight runs would be needed in order to have a 95% chance of passing the target acceptance criterion for relative bias if the true relative bias is zero. Note that the calculation of sample size assumes that a singlet of the validation samples will be performed in each validation run. The use of multiple replication sets and/or multiple assays will provide valuable information that allows separate estimates for intra-run and inter-run variability, and will decrease the risk of failing to meet the validation target acceptance criteria.
Five levels of the target analyte are studied in the validation: 0.50, 0.71, 1.00, 1.41, and 2.00. Two runs at each level are generated by two trained analysts using two media lots. Other factors may be considered and incorporated into the design using a fractional factorial layout. The laboratory should strive to design the validation with as many levels of each factor as possible in order to best model the long-term performance of the bioassay. In this example each analyst performs two runs at each level using each media lot. A run consists of a full dilution series of the Standard as described in the bioassay’s operating procedure, together with two independent dilution series of the Test sample. This yields duplicate measurements of relative potency in each run; see Table 4 for all relative potency observations. Note that the two potency estimates at each level of potency in a run are not independent due to common analysts and media lots.
Table 4. Example of Bioassay Validation with Two Analysts, Two Media Lots, and Runs per Level for Each Combination of Analyst and Lot
| Media Lot/Analyst |
1/1 | 1/2 | 2/1 | 2/2 | ||||
|---|---|---|---|---|---|---|---|---|
| Run | 1 | 2 | 1 | 2 | 1 | 2 | 1 | 2 |
| 0.50 | 0.5215 | 0.4532 | 0.5667 | 0.5054 | 0.5222 | 0.5179 | 0.5314 | 0.5112 |
| 0.50 | 0.5026 | 0.4497 | 0.5581 | 0.5350 | 0.5017 | 0.5077 | 0.5411 | 0.5488 |
| 0.71 | 0.7558 | 0.6689 | 0.6843 | 0.7050 | 0.6991 | 0.7463 | 0.6928 | 0.7400 |
| 0.71 | 0.7082 | 0.6182 | 0.8217 | 0.7143 | 0.6421 | 0.6877 | 0.7688 | 0.7399 |
| 1.00 | 1.1052 | 0.9774 | 1.1527 | 0.9901 | 1.0890 | 1.0314 | 1.1459 | 1.0273 |
| 1.00 | 1.1551 | 0.8774 | 1.1074 | 1.0391 | 0.9233 | 1.0318 | 1.1184 | 1.0730 |
| 1.41 | 1.5220 | 1.2811 | 1.5262 | 1.4476 | 1.4199 | 1.3471 | 1.4662 | 1.5035 |
| 1.41 | 1.5164 | 1.3285 | 1.5584 | 1.4184 | 1.4025 | 1.4255 | 1.5495 | 1.5422 |
| 2.00 | 2.3529 | 1.8883 | 2.3501 | 2.2906 | 2.2402 | 2.1364 | 2.3711 | 2.0420 |
| 2.00 | 2.2307 | 1.9813 | 2.4013 | 2.1725 | 2.0966 | 2.1497 | 2.1708 | 2.3126 |
A plot is used to reveal irregularities in the experimental results. In particular, a properly prepared plot can reveal a failure in agreement of validation results with validation levels, as well as heterogeneity of variability across levels (see discussion of the log transformation in section 2.7 Statistical Considerations). The example plot in Figure 3 includes the unit line (line with slope equal to 1, passing through the origin). The analyst 1 and analyst 2 data are deliberately offset with respect to the expected potency to allow clear visualization and comparison of the data sets from each analyst.
A formal analysis of the validation data might be undertaken in the following steps: (1) an assessment of variability (IP) should precede an assessment of relative accuracy or specificity in order to establish conformance to the assumption that variances across sample levels can be pooled; and (2) relative accuracy is assessed either at separate levels or by a combined analysis, depending on how well the data across levels can be pooled. These steps are demonstrated using the example validation data, along with some details of the calculations for illustrative purposes. Note that the calculations illustrated in the following sections are appropriate only with a balanced dataset. Imbalanced designs or datasets with missing relative potency measurements should be analyzed using a mixed model analysis with restricted maximum likelihood estimation (REML).
3.1 Intermediate Precision
Data at each level can be analyzed using variance component analysis. With balanced data, as in this example, variance components can be determined from a standard one-way ANOVA. An example of the calculation performed at a single level (0.50) is presented in Table 5.
Table 5. Variance Component Analysis Performed on Log Relative Potency Measurements at the 0.5 Level
| Source | df | Sum of Squares | Mean Square | Expected Mean Square |
|---|---|---|---|---|
| Run | 7 | 0.055317 | 0.007902 | Var(Error) + 2 Var(Run) |
| Error | 8 | 0.006130 | 0.000766 | Var(Error) |
| Corrected total | 15 | 0.061447 | ||
| Variance Component Estimates | ||||
| Var(Run) = 0.003568 | ||||
| Var(Error) = 0.000766 | ||||
The top of the table represents a standard ANOVA analysis. Analyst and media lot have not been included because of the small number of levels (2 levels) for each factor. The factor “Run” in this analysis represents the combined runs across the analyst by media lot combinations. The Expected Mean Square is the linear combination of variance components that generates the measured mean square for each source. The variance component estimates are derived by solving the equation “Expected Mean Square = Mean Square” for each component. To start, the mean square for Error estimates Var(Error), the within-run component of variability, is
Var(Error) = MS(Error) = 0.000766
The between-run component of variability, Var(Run), is subsequently calculated by setting the mean square for Run to the mathematical expression for the expected mean square, then solving the equation for Var(Run) as follows:
These variance component estimates are combined to establish the overall IP of the bioassay at 0.50:
The same analysis was performed at each level of the validation, and is presented in Table 6.
Table 6. Variance Component Estimates and Overall Variability for Each Validation Level and the Average
| Level | ||||||
|---|---|---|---|---|---|---|
| Component | 0.50 | 0.71 | 1.00 | 1.41 | 2.00 | Average |
| Var(Run) | 0.003568 | 0.000648 | 0.003639 | 0.003135 | 0.002623 | 0.002723 |
| Var(Error) | 0.000766 | 0.004303 | 0.002954 | 0.000577 | 0.002258 | 0.002172 |
| Overall | 6.8% | 7.3% | 8.5% | 6.3% | 7.2% | 7.2% |
A combined analysis can be performed if the variance components are similar across levels. Typically a heuristic method is used for this assessment. One might hold the ratio of the maximum variance to the minimum variance to no greater than 10 (10 is used because of the limited number of runs performed in the validation). Here the ratios associated with the between-run variance component, 0.003639/0.000648 = 5.6, and the within-run component, 0.004303/0.000577 = 7.5, meet the 10-fold criterion. Had the ratio exceeded 10 and if this was due to excess variability in one or the other of the extremes in the levels tested, that extreme would be eliminated from further analysis and the range would be limited to exclude that level.
The analysis might proceed using statistical software that is capable of applying a mixed effects model to the validation results. That analysis should account for any imbalance in the design, random effects such as analyst and media lot, and fixed effects such as level (see section 2.7 Statistical Considerations, Modeling Validation Results Using Mixed Effects Models). Variance components can be determined for analyst and media lot separately in order to characterize their contributions to the overall variability of the bioassay.
In the example, variance components can be averaged across levels to report the IP of the bioassay. This method of combining estimates is exact only if a balanced design has been employed in the validation (i.e., the same replication strategy at each level). A balanced design was employed for the example validation, so the IP can be reported as 7.2% GCV.
Because of the recommendation to report validation results with some measure of uncertainty, a one-sided 95% upper confidence bound can be calculated for the IP of the bioassay. The literature contains methods for calculating confidence bounds for variance components. The upper bound on IP for the bioassay example is 11.8% GCV. The upper confidence bound was not calculated at each level separately because of the limited data at an individual level relative to the overall study design.
3.2 Relative Accuracy
The analysis might proceed with an assessment of relative accuracy at each level. Table 7 shows the average and 90% confidence interval of validation results in the log scale, as well as corresponding potency and relative bias.
Table 7. Average Potency and Relative Bias at Individual Levels
| Log Potency | Potency | Relative Bias | |||||
|---|---|---|---|---|---|---|---|
| Level | na | Average | (90% CI) | Average | (90% CI) | Average | (90% CI) |
| 0.50 | 8 | –0.6613 | (–0.7034, –0.6192) | 0.52 | (0.49, 0.54) | 3.23% | (–1.02, 7.67) |
| 0.71 | 8 | –0.3419 | (–0.3773, –0.3064) | 0.71 | (0.69, 0.74) | 0.06% | (–3.42, 3.67) |
| 1.00b | 8 | 0.0485 | (0.0006, 0.0964) | 1.05 | (1.00, 1.10) | 4.97% | (0.06, 10.12) |
| 1.41 | 8 | 0.3723 | (0.3331, 0.4115) | 1.45 | (1.40, 1.51) | 2.91% | (–1.04, 7.03) |
| 2.00 | 8 | 0.7859 | (0.7449, 0.8269) | 2.19 | (2.11, 2.29) | 9.72% | (5.31, 14.32) |
|
a
Analysis performed on averages of duplicates from each run.
b
Calculation illustrated in section 2.7 Statistical Considerations, Scale of Analysis.
|
|||||||
The analysis has been performed on the average of the duplicates from each run (n = 8 runs) because duplicate measurements are correlated within a run by shared IP factors (analyst, media lot, and run in this case). A plot of relative bias versus level can be used to examine patterns in the experimental results and to establish conformance to the target acceptance criterion for relative bias (12%).
Figure 4. Plot of 90% confidence intervals for relative bias versus the acceptance criterion. Note lower acceptance criterion is equal to 100·[(1/1.12)  1] =
1] =  11%.
11%.
Figure 4 shows an average positive bias across sample levels (i.e., the average relative bias is positive at all levels). This consistency is due in part to the lack of independence of bioassay results across levels. In addition there does not appear to be a trend in relative bias across levels. The latter would indicate that a comparison of samples with different measured relative potency (such as stability samples) is biased, resulting perhaps in an erroneous conclusion. Trend analysis can be performed using a regression of log relative potency versus log level. Introduction during the development of the bioassay validation protocol of an acceptance criterion on a trend in relative accuracy across the range can be considered.
After establishing that there is no meaningful trend across levels, the analysis proceeds with an assessment of the relative accuracy at each level. The bioassay has acceptable relative bias at levels from 0.50 to 1.41, yielding 90% confidence bounds (equivalent to a two one-sided t-test) that fall within the acceptance region of  11% to 12% relative bias. The 90% confidence interval at 2.0 falls outside the acceptance region, indicating that the relative bias may exceed 12%.
11% to 12% relative bias. The 90% confidence interval at 2.0 falls outside the acceptance region, indicating that the relative bias may exceed 12%.
A combined analysis can be performed utilizing statistical software that is capable of applying a mixed effects model to the validation results. That analysis accurately accounts for the validation study design. The analysis also accommodates random effects such as analyst, media lot, and run (see section 2.7 Statistical Considerations, Modeling Validation Results Using Mixed Effects Models).
3.3 Range
The conclusions derived from the assessment of IP and relative accuracy can be used to establish the bioassay’s range that demonstrates satisfactory performance. Based on the acceptance criterion for IP equal to 8% GCV (see Table 6) and for relative bias equal to 12% (see Table 7), the range of the bioassay is 0.50 to 1.41. In this range, level 1.0 has a slightly higher than acceptable estimate of IP (8.5% versus the target acceptance criterion  8.0%), which may be due to the variability of the estimate that results from a small dataset. Because of this and other results in Table 6, one may conclude that satisfactory IP was demonstrated across the range.
8.0%), which may be due to the variability of the estimate that results from a small dataset. Because of this and other results in Table 6, one may conclude that satisfactory IP was demonstrated across the range.
3.4 Use of Validation Results for Bioassay Characterization
When the study has been performed to estimate the characteristics of the bioassay (characterization), the variance component estimates can also be used to predict the variability for different bioassay formats and thereby can determine a format that has a desired level of precision. The predicted variability for k independent runs, with n individual dilution series of the test preparation within a run, is given by the following formula for format variability:
Format Variability = 100·(e Var(Run)/k + Var(Error)/(nk)
Var(Run)/k + Var(Error)/(nk)  1)
1)
Using estimates of intra-run and inter-run variance components from Table 6 [Var(Run) = 0.002723 and Var(Error) = 0.002172], if the bioassay is performed in three independent runs, the predicted variability of the reportable value (geometric mean of the relative potency results) is equal to:
Format Variability = 100·(e  0.002723/3 + 0.002172/(1·3)
0.002723/3 + 0.002172/(1·3)  1) = 4.1%
1) = 4.1%
This calculation can be expanded to include various combinations of runs and minimal sets (assuming that the numbers of samples, dilutions, and replicates in the minimal sets are held constant) within runs as shown in Table 8.
Table 8. Format Variability for Different Combinations of
Number of Runs (k) and Number of
Minimal Sets within Run (n)
Number of Runs (k) and Number of
Minimal Sets within Run (n)
| Number of Runs (k) | ||||
|---|---|---|---|---|
| Reps (n) | 1 | 2 | 3 | 6 |
| 1 | 7.2% | 5.1% | 4.1% | 2.9% |
| 2 | 6.4% | 4.5% | 3.6% | 2.6% |
| 3 | 6.0% | 4.2% | 3.4% | 2.4% |
| 6 | 5.7% | 4.0% | 3.3% | 2.3% |
Clearly the most effective means of reducing the variability of the reportable value (the geometric mean potency across runs and minimal sets) is by independent runs of the bioassay procedure. In addition, confidence bounds on the variance components used to derive IP can be utilized to establish the bioassay’s format variability.
Significant sources of variability must be incorporated into runs in order to effect variance reduction. A more thorough analysis of the bioassay validation example would include analyst and media lot as factors in the statistical model. Variance component estimates obtained from such an analysis are presented in Table 9.
Table 9. REML Estimates of Variance Components Associated
with Analyst, Media Lot, and Run
with Analyst, Media Lot, and Run
| Variance | Component Estimate |
|---|---|
| Var(Media Lot) | 0.0000 |
| Var(Analyst) | 0.0014 |
| Var(Analyst*Media Lot) | 0.0000 |
| Var(Run (Analyst*Media Lot)) | 0.0019 |
| Var(Error) | 0.0022 |
Identification of analyst as a significant bioassay factor should ideally be addressed during bioassay development. Nonetheless the laboratory may choose to address the apparent contribution of analyst-to-analyst variability through improved training or by using multiple analysts in formatting the assay for routine performance of the bioassay.
Estimates of intra-run and inter-run variability can also be used to determine the sizes of differences (fold difference) that can be distinguished between samples tested in the bioassay. For k runs, with n minimal sets within each run, using an approximate two-sided critical value from the standard normal distribution with z = 2, the critical fold difference between reportable values for two samples that are tested in the same runs of the bioassay is given by:
Critical Fold Difference = e2 ·  Var(Run)/k+Var(Error)/(nk)
Var(Run)/k+Var(Error)/(nk)
When samples have been tested in different runs of the bioassay (such as long-term stability samples), the critical fold difference is given by (assuming the same format is used to test the two series of samples):
Critical Fold Difference = e2· 2·[Var(Run)/k+Var(Error)/(nk)]
2·[Var(Run)/k+Var(Error)/(nk)]
For comparison of samples the laboratory can choose a design (bioassay format) that has suitable precision to detect a practically meaningful fold difference between samples.
3.5 Confirmation of Intermediate Precision and Revalidation
The estimate of IP from the validation is highly uncertain because of the small number of runs performed. After the laboratory gains suitable experience with the bioassay, the estimate can be confirmed or updated by analysis of control sample measurements such as the variability of a positive control. This analysis can be done with the control prepared and tested like a Test sample (i.e., same or similar dilution series and replication strategy). This assessment should be made after sufficient assays have been performed to obtain an alternative estimate of the bioassay’s intermediate precision, including implementation of changes (e.g., different analysts, different key reagent lots, and different cell preparations) associated with the standardized assay protocol. The reported IP of the bioassay should be modified as an amendment to the validation report if the assessment reveals a substantial disparity of results.
The bioassay should be revalidated whenever a substantial change is made to the method. This includes but is not limited to a change in technology or a change in readout. The revalidation may consist of a complete re-enactment of the bioassay validation or a bridging study that compares the current and the modified methods.
4. ADDITIONAL SOURCES OF INFORMATION
Additional information and alternative methods can be found in the references listed below.
- ASTM. Standard Practice for Using Significant Digits in Test Data to Determine Conformance with Specifications, ASTM E29-08. Conshohocken, PA: ASTM; 2008.
- Berger R, Hsu J. Bioequivalence trials, intersection-union tests and equivalence confidence intervals. Stat Sci 1996;11(4):283–319.
- Burdick R, Graybill F. Confidence Intervals on Variance Components. New York: Marcel Dekker; 1992:28–39.
- Haaland P. Experimental Design in Biotechnology. New York: Marcel Dekker; 1989;64–66.
- Schofield TL. Assay validation. In: Chow SC, ed. Encyclopedia of Biopharmaceutical Statistics. 2nd ed. New York: Marcel Dekker; 2003.
- Schofield TL. Assay development. In: Chow SC, ed. Encyclopedia of Biopharmaceutical Statistics. 2nd ed. New York: Marcel Dekker; 2003.
- Winer B. Statistical Principles in Experimental Design. 2nd ed. New York: McGraw-Hill; 1971:244–251.
APPENDIX—MEASURES OF LOCATION AND SPREAD FOR LOG NORMALLY DISTRIBUTED VARIABLES
Two assumptions of common statistical procedures, such as ANOVA or confidence interval estimation, are (1) the variation in the bioassay response about its mean is normally distributed and (2) the standard deviation of the observed response values is constant over the range of responses that are of interest. Such responses are said to have a “normal distribution” and an “additive error structure”. When these two conditions are not met, it may be useful to consider a transformation before using common statistical procedures.
The variation in bioassay responses is often found to be non-normal (skewed toward higher values) with a standard deviation approximately proportional (or nearly so) to the mean response. Such responses often have a “multiplicative error structure” and follow a “log normal distribution” with a percent coefficient of variation (%CV) that is constant across the response range of interest. In such cases, a log transformation of the bioassay response will be found to be approximately normal with a nearly constant standard deviation over the response range. After log transformation, then, the two assumptions are met, and common statistical procedures can be performed on the log transformed response. The following discussion presumes a log normal distribution for the bioassay response.
We refer to an observed bioassay response value, X, as being on the “original scale of measurement” and to the log transformed response, Y = log(X), as being on the “log transformed scale”. Although common statistical procedures may be appropriate only on the log transformed scale, we can summarize bioassay response results by estimating measures of location (e.g., mean or median), measures of spread (e.g., standard deviation), or confidence intervals on either scale of measurement, as long as the scale being used is indicated. The %CV is useful on the original scale where it is constant over the response range. For the same reason, the standard deviation (SD) is relevant on the log transformed scale. There may be advantages to reporting statistical summaries on the basis of the log transformed (Y) scale. However, it is often informative to back transform the reported measures to the original scale of measurement (X).
For any given value of X, there is only one unique value of Y = log(X), and vice versa. Similarly for measures of location and spread, there is a unique one-to-one correspondence between measures of location and spread obtained on the original and log transformed scales. Further, just as there is a simple relationship between X and Y = log(X), there are relatively simple relationships that allow conversion between the corresponding measures on each scale, as indicated in Table A-1 below. In the table, “Average” and “SD”, wherever they appear, refer to measures calculated on the log transformed (Y) scale.
Table A-1. Comparison of Measures of Location and Spread
| Measure | Scale of Measurement | ||
|---|---|---|---|
| Log Transformed (V) | Original (X) | ||
| Location | Mean (average) | Geometric mean (GM) | |
| Spread | Standard deviation (SD) | Geometric standard deviation (GSD) = eSD |
|
| Confidence intervals (k is an appropriate constant based on the t-distribution or large sample z approximation) |
Lower | Average |
GM/GSDk/ |
| Upper | Average + k · SD/ |
GM · GSDk/ |
|
| Size | Width (upper = 2 · k · SD/ |
Ratio(upper/lower) = GSD2k/ |
|
| Percent coefficient of variation (%CV) |
%GCV = 100 · (GSD |
||
The geometric mean (GM) should not be misinterpreted as an estimate of the mean of the original scale (X) variable, but is instead an estimate of the median of X. The median is a more appropriate measure of location for variables with skewed error distributions such as the log normal, as well as symmetric error distributions where the median is equal to the mean.
Similarly, the geometric standard deviation (GSD) should not be misinterpreted as the standard deviation of the original scale (X) variable. GSD is, however, a useful multiplicative factor for obtaining confidence intervals on the original (X) scale that correspond to those on the log transformed (Y) scale, as shown in the above table. A GSD of 1 corresponds to no variation (SD of Y = 0). The ratio of the Upper to the Lower confidence bounds, on the untransformed (X) scale, will be equal to GSD2k/ n, as can be seen from Table A-1.
n, as can be seen from Table A-1.
The geometric coefficient of variation (%GCV) approximates the %CV on the original (X) scale when the %CV is below 20%. It is important not to confuse these different measures of spread. The %GCV is a measure relevant to the log transformed (Y) scale, and the %CV is a measure relevant to the original (X) scale. Depending on the preferred frame of reference, either or both measures may be useful.
APPENDIX INFORMATION SOURCES
- Limpert E, Stahel WA, Abbt M. (2001) Log-normal distributions across the sciences: keys and clues. BioScience 51(5): 341–252.
- Kirkwood TBL. (1979) Geometric means and measures of dispersion. Biometrics 35: 908–909.
- Bohidar NR. (1991) Determination of geometric standard deviation for dissolution. Drug Development and Industrial Pharmacy 17(10): 1381–1387.
- Bohidar NR. (1993) Rebuttal to the “Reply”. Drug Development and Industrial Pharmacy 19(3): 397–399.
- Kirkwood TBL. (1993) Geometric standard deviation—reply to Bohidar. Drug Development and Industrial Pharmacy 19(3): 395–396.
-
 1010
1010 Analytical data: interpretation and treatment. USP 34. In: USP34–NF 29. Vol. 1. Rockville (MD): United States Pharmacopeial Convention; c2011. p. 419.
Analytical data: interpretation and treatment. USP 34. In: USP34–NF 29. Vol. 1. Rockville (MD): United States Pharmacopeial Convention; c2011. p. 419.
- Tan CY. (2005) RSD and other variability measures of the lognormal distribution. Pharmacopeial Forum 31(2): 653–655.
Auxiliary Information—
Please check for your question in the FAQs before contacting USP.
| Topic/Question | Contact | Expert Committee |
|---|---|---|
| General Chapter | Tina S. Morris, Ph.D.
Vice President, Biologics & Biotechnology (301) 816-8397 |
(STAT2010) Statistics 2010 |
USP38–NF33 Page 787
Pharmacopeial Forum: Volume No. 36(4) Page 986





























