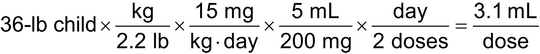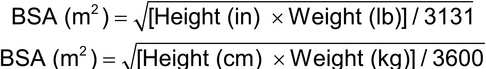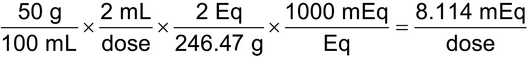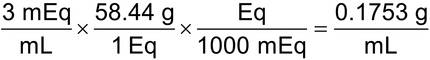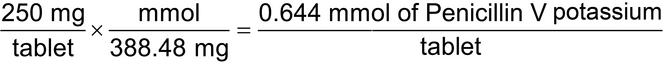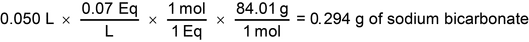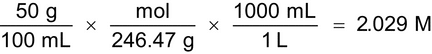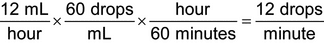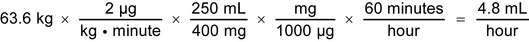Change to read:
1160 PHARMACEUTICAL CALCULATIONS IN PHARMACY PRACTICE1S (USP38)

1. INTRODUCTION
The purpose of this general chapter is to provide general information to assist pharmacists and support personnel in performing the necessary calculations for compounding and dispensing medications. This general chapter is not inclusive of all the information necessary for performing pharmaceutical calculations. For additional information regarding pharmaceutical calculations, consult a pharmaceutical calculations textbook. For additional information on pharmaceutical compounding and drug stability, see: Pharmaceutical Compounding—Nonsterile Preparations 795, Pharmaceutical Compounding—Sterile Preparations 797, and Packaging and Storage Requirements 659; Quality Assurance in Pharmaceutical Compounding 1163 and Stability Considerations in Dispensing Practice 1191.
Correct pharmaceutical calculations can be accomplished by using proper conversions from one measurement system to another and properly placing decimal points (or commas, in countries where it is customary to use these in the place of decimal points), by understanding the arithmetical concepts, and by paying close attention to the details of the calculations. Before proceeding with any calculation, pharmacists should do the following: (a) read the entire formula or prescription carefully; (b) determine the materials that are needed; and then (c) select the appropriate methods of preparation and the appropriate calculations.
Logical methods that require as few steps as possible should be selected to ensure that calculations are done accurately and correctly. A pharmacist should double-check each calculation or have someone else double-check, e.g., a technician, if another pharmacist is not available, before proceeding with compounding the preparation. One expedient method of double-checking is estimation, which consists of convenient rounding (e.g., 0.012 to 0.01, 0.44 to 0.5, 18.3 to 20, and 476 to 500) to approximate the magnitude of answers.

2. CALCULATING AMOUNTS OF ACTIVE INGREDIENTS
The pharmacist must be able to calculate the amount or concentration of drug substances in each unit or dosage portion of a compounded preparation at the time it is prepared and again at the time it is dispensed. Pharmacists must perform calculations and measurements to obtain, theoretically, 100% of the amount of each ingredient in compounded formulations. Calculations must account for the active ingredient, or active moiety, and water content of drug substances, which includes that in the chemical formulas of hydrates. Official drug substances and added substances must meet the requirements in general chapter Loss on Drying 731, which must be included in the calculations of amounts and concentrations of ingredients. The pharmacist should consider the effect of ambient humidity on the gain or loss of water from drugs and added substances in containers subjected to intermittent opening over prolonged storage. Each container should be opened for the shortest duration necessary and then closed tightly immediately after use.
The nature of the drug substance to be weighed and used in compounding a prescription must be known. If the substance is a hydrate, its anhydrous equivalent weight may need to be calculated. On the other hand, if there is adsorbed moisture present that is either specified on a Certificate of Analysis (CoA) or that is determined in the pharmacy immediately before the drug substance is used in the preparation (see chapter 731), this information must be used when calculating the amount of drug substance that is to be weighed to determine the exact amount of anhydrous drug substance required.
There are cases in which the required amount of a dose is specified in terms of a cation (e.g., Li+), an anion (e.g., F–), or a molecule (e.g., theophylline in aminophylline). In these instances, the drug substance weighed is a salt or complex, a portion of which represents the pharmacologically active moiety. Thus, the exact amount of such substances weighed must be calculated on the basis of the required quantity of the pharmacological moiety.
The following formula may be used to calculate the theoretical weight of an ingredient in a compounded preparation:
W = AB/CD

W = actual weighed amount
A = prescribed or pharmacist-determined weight of the active or functional moiety of drug or added substance
B = molecular weight (MW) of the ingredient, including waters of hydration for hydrous ingredients
C = MW of the active or functional moiety of a drug or added substance that is provided in the MW of the weighed ingredient
D = the fraction of dry weight when the percent by weight of adsorbed moisture content is known from the loss on drying procedure (see chapter 731) or from the CoA. The CoA should be lot specific.
2.1 Active Ingredients
2.1.1 calculating drugs dosed as salt form and hydrate
Examples—Drugs dosed as salt form and hydrate
1. Drugs dosed as salt form and hydrate
Triturate morphine sulfate and lactose to obtain 10 g in which there are 30 mg of morphine sulfate for each 200 mg of the morphine–lactose mixture. [Note—Morphine is dosed as the morphine sulfate, which is the pentahydrate. ]

W= weight of morphine sulfate (g)
A= weight of morphine sulfate pentahydrate in the prescription, 1.5 g
B= MW of morphine sulfate pentahydrate, 759 g/mol
C= MW of morphine sulfate pentahydrate, 759 g/mol
D= 1.0
To solve the equation:
W = (1.5 g × 759 g/mol)/(759 g/mol × 1) = 1.5 g of morphine sulfate pentahydrate
2. Active drug moiety and correction for moisture
Accurately weigh an amount of aminophylline to obtain 250 mg of anhydrous theophylline. [Note—In this example, the powdered aminophylline dihydrate weighed contains 0.4% w/w absorbed moisture as stated in the CoA received by the pharmacy. ]
W = AB/CD

W= weight of aminophylline dihydrate (mg)
A= weight of anhydrous theophylline, 250 mg
B= MW of aminophylline dihydrate, 456 g/mol
C= MW of anhydrous theophylline, 360 g/mol
D= 0.996
[Note—One mol of aminophylline contains 2 mol of theophylline. Theophylline has a MW of 180. ]
To solve the equation:
W = (250 mg × 456 g/mol)/(360 g/mol × 0.996) = 318 mg of aminophylline dihydrate
2.2 Hydrates, Salts, and Esters
Frequently, for stability or other reasons such as taste or solubility, the base form of a drug is administered in another form such as a salt or an ester. This altered form of the drug usually has a different MW, and at times it may be useful to determine the amount of the base form of the drug in the altered form.
2.2.1 calculating hydrates, salts, and esters
Examples—Hydrates, salts, and esters
1. Hydrates
If a prescription for 100 g of lidocaine hydrochloride 2% gel is to be made, 2 g of anhydrous lidocaine hydrochloride could be used, or the equivalent amount of lidocaine hydrochloride monohydrate could be calculated as follows:

W= weight of lidocaine hydrochloride monohydrate (g)
A= weight of anhydrous lidocaine hydrochloride in the prescription, 2 g
B= MW of lidocaine hydrochloride monohydrate, 288.81 g/mol
C= MW of anhydrous lidocaine hydrochloride, 270.80 g/mol
D= 1.0
To solve the equation:
W = (2 g × 288.81 g/mol)/(270.80 g/mol × 1) = 2.133 g of lidocaine hydrochloride monohydrate
2. Salts
A prescription calls for 10 mL of a fentanyl topical gel at a concentration 50 µg fentanyl/0.1 mL prepared from fentanyl citrate. The amount of fentanyl citrate required for the preparation could be calculated as follows:
Amount of fentanyl needed for the preparation:
(50 µg fentanyl/0.1 mL) × 10 mL = 5000 µg of fentanyl

W= weight of fentanyl citrate in the prescription (µg)
A= weight of fentanyl in the prescription, 5000 µg
B= MW of fentanyl citrate, 528.59 g/mol
C= MW of fentanyl, 336.47 g/mol
D= 1.0
To solve the equation:
W = (5000 µg × 528.59 g/mol)/(336.47 g/mol × 1) = 7855 µg of fentanyl citrate
3. Esters
The amount of cefuroxime axetil contained in a single 250-mg cefuroxime tablet can be calculated as follows:

W= weight of cefuroxime axetil in tablet (mg)
A= weight of cefuroxime in the prescription, 250 mg
B= MW of cefuroxime axetil, 510.47 mg/mmol
C= MW of cefuroxime, 424.39 mg/mmol
D= 1.0
To solve the equation:
W = (250 mg × 510.47 g/mol)/(424.39 g/mol × 1) = 300 mg of cefuroxime axetil

3. DOSAGE CALCULATIONS
3.1 Dosing by Weight
Doses are frequently expressed as mg of drug per kg of body weight per a dosing interval.
3.1.1 calculating dosing by weight
Example—Dosing by weight
A physician orders azithromycin for oral suspension at a dose of 15 mg/kg/day, divided every 12 h, for a child that weighs 36 lb. Calculate the volume of oral suspension, in mL, that should be administered for each dose of a 200-mg/5-mL suspension as follows:
  1. Calculate the child's weight in kg:
    36 lb × kg/2.2 lb = 16.4 kg
  2. Multiply the weight, in kg, by the dosing rate:
    16.4 kg × 15 mg/kg/day = 246 mg/day
  3. Divide the total daily dose by the number of doses/day:
    246 mg/2 doses = 123 mg/dose
  4. Calculate the volume of each dose using ratio and proportion:
    (123 mg/dose)/(200 mg/5 mL) = 3.1 mL/dose
Some calculations may also be completed using dimensional units analysis (DUA). The DUA should begin at the left end with a factor containing the numerator answer units. All units other than those in the answer should cancel. If using DUA, the preceding equation would be as follows:
Click to View Image
3.2 Dosing by Body Surface Area (Humans)
Some medications, including chemotherapeutic agents, require dosing by body surface area (BSA). The dose is expressed as amount of drug per meter squared (m2). BSA may be calculated using the following formulas:
Click to View Image
3.2.1 calculating by body surface area (human)
Example—Dosing by BSA (humans)
A physician orders rituximab at a dose of 375 mg/m2 every week for 6 weeks for a patient who is 6 ft 2 in tall and weighs 183 lb. Calculate the volume, in mL, of 10-mg/mL rituximab injection needed to make each IV infusion dose as follows:
  1. Calculate the patient’s BSA:
    Click to View Image
  2. Multiply the BSA by the dosing rate:
    2.08 m2 × 375 mg/m2 = 780 mg/dose
  3. Calculate the volume of each dose using ratio and proportion:
    (780 mg/dose)/(10 mg/mL) = 78 mL/dose
The preceding calculation may also be completed using DUA as follows:
Click to View Image
3.3 Dosing By Body Surface Area (Animals)
BSA for cats and dogs may be calculated using the following formulas. For other animals, consult an appropriate veterinary medicine reference.
Body surface area for cats:
BSA (m2) = {10 × [body weight (g)]0.667}/10,000
Body surface area for dogs:
BSA (m2) = {10.1 × [body weight (g)]0.667}/10,000
3.3.1 calculating dosing by body surface area (animals)
Example—Dosing by BSA (animals)
A veterinarian orders oral cyclophosphamide therapy at a dose of 50 mg/m2 for a cat who weighs 5.8 kg. Calculate the dose of cyclophosphamide as follows:
  1. Calculate the cat’s BSA:
    BSA (m2) = [10 × (5800 g)0.667]/10,000 = 0.324 m2
  2. Multiply the BSA by the dosing rate:
    0.324 m2 × 50 mg/m2 = 16.2 mg

4. USE OF POTENCY UNITS
Because some substances cannot be completely characterized by chemical and physical means, it may be necessary to express quantities of activity in biological units of potency [see the USP General Notices and Requirements 5.50.10, Units of Potency (Biological)].
4.1 Calculating by Use of Potency Units
Examples—Use of potency units
1. Potency units-to-milligrams conversion
A dose of penicillin G benzathine for streptococcal infection is 1.2 million units administered intramuscularly. If a specific product contains 1180 units/mg, calculate the amount, in mg, of penicillin G benzathine in the dose as follows:
(1,200,000 units)/(1180 units/mg) = 1017 mg of penicillin G benazathine
2. Potency units-to-milligrams conversion
A prescription calls for 60 g of an ointment containing 150,000 units of nystatin per gram. Calculate the quantity of nystatin with a potency of 4400 units/mg that should be weighed for the prescription as follows:
60 g × (150,000 units of nystatin/g) = 9,000,000 units
9,000,000 units/(4400 units/mg) = 2045 mg of nystatin

5. VOLUME AND WEIGHT SUMS
Weights are additive in most mixtures of liquids, semisolids, and solids. Volumes in mixtures of miscible solutions and pure liquids may or may not be additive, based primarily on the effects of volume proportions and intermolecular hydrogen bonding. For example, mixtures containing equal or near-equal volumes of water and ethanol (and other miscible mono-hydroxy alcohols) will be exothermic and result in a volume contraction of <5%, e.g., 50 mL water + 50 mL ethanol yield 97–98 mL at 20–25. Negligible volume contraction occurs between water and polyhydroxy or polyhydric alcohols, e.g., glycerin and propylene glycol. Volumes are additive with usually negligible error in aqueous mixtures that contain <10% of mono-hydroxy alcohols, i.e., there is <0.5% volume contraction.

6. DENSITY AND SPECIFIC GRAVITY
Density is defined as the mass of a substance in air at a specific temperature (typically 25) per unit volume of that substance at the same temperature. Density may be calculated with the following equation:
Density = (mass of substance/volume of substance) at a particular temperature and pressure
Specific gravity (SG) is the unitless ratio of the density of a substance to the density of water at 4, or [(g of substance/mL)/1.00 g/mL]. Alternatively, SG can be calculated at a particular temperature in some common units of density from density of substance per density of water.
SG may be calculated with the following equation:
SG = (weight of the substance)/(weight of an equal volume of water)
6.1 Calculating Density and Specific Gravity
Examples—Density and specific gravity
1. Density calculation
2.3 g of activated charcoal powder occupies a bulk volume of 5.2 mL at 20 and 1 atm. The density of activated charcoal powder can be calculated as follows:
Density = 2.3 g/5.2 mL = 0.44 g/mL
2. SG calculation
125 g of glycerin occupies a volume of 99 mL at 25. [Note—The density of water at 25 is 0.997 g/mL. ] The SG of glycerin can be calculated as follows:
SG = (125 g/99 mL)/(0.997 g/mL) = 1.266
3. Concentrated acid calculation
Hydrochloric acid is approximately a 37% w/w solution of hydrochloric acid in water. Calculate the amount, in g, of hydrochloric acid contained in 75 mL of hydrochloric acid as follows. [Note—The SG of hydrochloric acid is 1.18. ]
37% w/w × 1.18 = 43.7% w/v
(43.7 g/100 mL) × 75 mL = 32.8 g of hydrochloric acid

7. MILLIEQUIVALENTS AND MILLIMOLES
[Note—This section addresses milliequivalents (mEq) and millimoles (mmol) as they apply to electrolytes for dosage calculations. See also the 8. Concentrations Expressions section of this chapter. ]
The quantities of electrolytes administered to patients are usually expressed in terms of mEq. Weight units such as mg or g are not often used for electrolytes because the electrical properties of ions are best expressed as mEq. An equivalent (Eq) is the weight of a substance that supplies 1 unit of charge. An equivalent weight is the weight, in g, of an atom or radical, divided by the valence of the atom or radical. A mEq is 1/1000th of an Eq. The equivalent weight of a compound may be determined by dividing its formula or MW in g by the valence of its largest valence ion.
A mole equals one gram-atomic weight or gram-molecular weight of a substance. A millimole equals 1/1000th of a mole.
7.1 Calculating Milliequivalents and Millimoles
Examples—Milliequivalents and millimoles
1.Calculate the mEq weight of calcium. [Note—Calcium has a MW of 40.08, and the valence of calcium is 2+. ]
Eq weight = 40.08 g/2 = 20.04 g
mEq weight = 20.04 g/1000 = 0.02004 g = 20.04 mg
2.Calculate the quantity, in mEq, of potassium in a 250-mg Penicillin V Potassium Tablet. [Note—Penicillin V potassium has a MW of 388.48 g, there is one potassium atom in the molecule, and the valence of potassium is 1+. ]
Eq weight = 388.48 g/1 = 388.48 g
mEq weight = 388.48 g/1000 = 0.38848 g = 388.48 mg
(250 mg/tablet)/(388.48 mg/mEq) = 0.644 mEq of potassium/tablet
3. Calculate the mEq of magnesium and sulfate in a 2-mL dose of 50% Magnesium Sulfate Injection. [Note—Magnesium sulfate (MgSO4·7H2O) has a MW of 246.47, and the highest valence ion is magnesium 2+ and sulfate 2–. ]
(50 g/100 mL) × (2 mL/dose) = 1 g/dose
Eq weight = 246.47 g/2 = 123.24 g/Eq
(1g/dose)/(123.24 g/Eq) = 0.008114 Eq = 8.114 mEq of both magnesium and sulfate per dose
This problem may also be worked using DUA as follows:
Click to View Image
4.A vial of sodium chloride injection contains 3 mEq/mL of sodium chloride. Calculate the strength, in % w/v, of the injection. [Note—Sodium chloride has a MW of 58.44. ]
Click to View Image
(0.1753 g/mL) × 100 mL = 17.53 g in 100 mL = 17.53% w/v
5.Calculate the weight of potassium in mmol. [Note—Potassium has a MW of 39.1. ]
The weight of 1 mol is 39.1 g and the weight in mmol is:
39.1 g/1000 = 0.0391 g or 39.1 mg
6.Calculate the mmol of penicillin V potassium in a 250-mg Penicillin V Potassium Tablet. [Note—Penicillin V potassium has a MW of 388.48. ]
The weight of 1 mol is 388.48 g, and the weight of 1 mmol is:
388.48 g/1000 = 0.38848 g or 388.48 mg
Click to View Image

8. CONCENTRATION EXPRESSIONS
The concentration expressions in this section refer to homogeneous mixtures of the following states of matter at a temperature of 20–30 and pressure of 1 atm (29.92 in Hg, 760 mm Hg, 101.3 kPa, 1013.3 mb): gas in gas, gas in liquid, liquid in liquid, liquid in semisolid, solid in liquid, solid in semisolid, and solid in solid. Concentration expressions used in pharmacy practice and pharmaceutical research include, but are not limited to, those listed in Table 1. Common metric drug strength and clinical concentrations include, for example, µg/mL, mg/dL, g or mg per L, and ng/µL (see General Notices and Requirements 8.240, Weights and Measures).
Table 1
Title Abbreviation Definition
Mass in volume ratios None is standard Mass of a dispersed or dissolved ingredient per volume amount of mixtures containing that ingredient
mEqa per volume mEq/volume unit mEq of an electrolyte or salt per unit of volume of solutions containing that electrolyte or salt
Molality m molb of a solute/kg of a solvent containing that solutec
Molarity M mol of a solute/L of a solvent containing that soluted
Normalitye N Equivalents (Eqf) of a solute/L of a solvent containing that soluteg
Parts per million ppm Parts of a gas, liquid, or solid per 1 million part of another gas, liquid, or solid containing the first gas, liquid, or solid
% Volume in volume % v/v mL of liquid per 100 mL of a solvent containing that liquid
% Weight in volume % w/v g of a solute per 100 mL of a solvent containing that solute
% Weight in weight % w/w g of a solute per 100 g of a mixture containing that solute
Ratio strength 1:R 1 part of an ingredient per Rh parts of a mixture containing that ingredient
1 in R 1 part of an ingredient in Rh parts of a mixture containing that ingredient
X:Y Xh parts of one ingredient per Yh parts of another ingredient in a mixture
a   1 mEq = Eq/1000.
b   The abbreviation for mole is mol.
c   1 mol of solute per 1 kg of solvent is a 1 molal (1 m) solution.
d   1 mol of solute per 1 L of solution of that solute is a 1 molar (1 M) solution.
e   Normality = (Molarity × largest valence ion of a compound), e.g., (18 M H2SO4 × 2) = 36 N H2SO4, where 2 derives from the 2– valence of SO4.
f   Eq of a compound = (1 mol × largest valence ion of a compound), e.g., 1 mol of lithium citrate = 3 Eq of lithium citrate; 1 mol of Ca(gluconate)2 = 2 Eq of Ca(gluconate)2; and 1 mol of KCl = 1 Eq of KCl.
g   1 Eq of solute per 1 L of solution of that solute is a 1 normal (1 N) solution.
h   R, X, and Y are whole numbers.
8.1 Calculating Normality
Example—Normality
Calculate the amount of sodium bicarbonate powder needed to prepare 50 mL of a 0.07 N solution of sodium bicarbonate (NaHCO3). [Note—Sodium bicarbonate has a MW of 84.01. ] In an acid or base reaction, because NaHCO3 may act as an acid by giving up one proton, or as a base by accepting one proton, one Eq of NaHCO3 is contained in each mole of NaHCO3.
Click to View Image
8.2 Calculating Percentage Concentrations
Percentage concentrations of solutions and other homogeneous mixtures are usually expressed in one of three common forms in which numerator and denominator quantities are in g and mL measurement units.
  1. Volume percent (% v/v) = (volume of liquid solute/volume of solution or suspension) × 100
    or % v/v = mL of liquid solute in 100 mL of solution or suspension
  2. Weight percent (% w/w) = (weight of solute/weight of mixture) × 100
    or % w/w = g of ingredient in 100 g of mixture
  3. Weight in volume percent (% w/v) = (weight of solute/volume of solution or suspension) × 100
    or % w/v = g of solute in 100 mL of solution or suspension
The preceding three equations may be used to calculate any one of the three values (i.e., weights, volumes, or percentages) in a given equation if the other two values are known (see also General Notices and Requirements 8.140, Percentage Concentrations).
Examples—Percentage concentrations
1. Weight percent
A prescription order reads as follows (see Table 2):
Table 2
Zinc oxide 7.5 g
Calamine 7.5 g
Starch 15 g
White petrolatum 30 g
Calculate the percentage concentration for each of the four components using the preceding weight percent equation as follows:
  1. The total weight of ointment = 7.5 g + 7.5 g + 15 g + 30 g = 60.0 g
  2. The weight percent of zinc oxide = (7.5 g of zinc oxide/60 g of ointment) × 100% = 12.5%
  3. The weight percent of calamine = (7.5 g of calamine/60 g of ointment) × 100% = 12.5%
  4. The weight percent of starch = (15 g of starch/60 g of ointment) × 100% = 25%
  5. The weight percent of white petrolatum = (30 g of white petrolatum/60 g of ointment) × 100% = 50%
2. Volume percent
A prescription order reads as follows:
Rx: Eucalyptus Oil 3% v/v in Mineral Oil.
Dispense 30 mL.
Calculate the quantities of ingredients in this prescription using the volume percent equation as follows:
  1. The amount of eucalyptus oil.
    3% v/v = (volume of oil in mL/30.0 mL) × 100%
    volume in oil = 0.9 mL of eucalyptus oil
  2. The amount of mineral oil.
    30 mL 0.9 mL = 29.1 mL of mineral oil
8.3 Conversions of Concentration Expressions
8.3.1 solid-in-liquid solution conversions
The calculations used to convert from percent weight in volume, % w/v, to other concentrations and vice versa, using the same densities and formula or molecular weights, are illustrated as follows for calcium chloride, magnesium sulfate, and potassium chloride solutions in water.
8.3.1.1 Calculating solid-in-liquid conversions
Examples—Solid-in-liquid conversions
1. Convert 10% w/v calcium chloride (CaCl2·2H2O) to molality (m). [Note—Calcium chloride has a MW of 147.01 g; 10% w/v solution has a density of 1.087 g/mL. ]
10% w/v = 10 g of calcium/100 mL of solution
Using the density of the solution:
100 mL of solution × 1.087 g/mL = 108.7 g of solution
108.7 g of solution 10 g of calcium chloride = 98.7 g of water = 0.0987 kg of water
10 g of calcium chloride/(147.01 g of calcium chloride/mol of calcium chloride) = 0.068 mol of calcium chloride
0.068 mol of calcium chloride/0.0987 kg of water = 0.689 m
2. Convert 50% w/v magnesium sulfate (MgSO4·7H2O) to molarity (M). [Note—Magnesium sulfate has a MW of 246.47 g. ]
Click to View Image
3. Convert 10% w/v calcium chloride (CaCl2·2H2O) to normality (N).
Click to View Image
*2 Eq/mol derived from the 2+ valence of calcium
4. Convert 10% w/v calcium chloride (CaCl2·2H2O) to mEq/mL.
Click to View Image
5. Convert 0.1% w/v calcium chloride (CaCl2·2H2O) to ppm.
(0.1 g/100 mL) × (1 × 106 ppm) = 1000 ppm
6. Convert 33% w/v potassium chloride (KCl) to 1:R ratio strength.
(1/R) = (33 g/100 mL)
R = 3.03
1:R = 1:3
8.3.2 liquid-in-liquid solution conversions
The calculations used to convert from percent weight in weight, % w/w, and volume in volume, % v/v, to other concentrations and vice versa using the same densities and formula or MWs, are illustrated for glycerin and isopropyl alcohol in water. Besides liquid-in-semisolid, solid-in-semisolid, and solid-in-solid mixtures, % w/w is used for viscous liquids, such as coal tar, glycerin, and concentrated acids.
8.3.2.1 Converting liquid-in-liquid solutions
Examples—Liquid-in-liquid conversions
1. Convert 50% w/w glycerin to % w/v. [Note—50% w/w glycerin has a density of 1.13 g/mL. ]
(50 g/100 g) × (1.13 g/mL) = 0.565 g/mL
56.5 g/100 mL = 56.5% w/v
2.Convert 70% v/v isopropyl alcohol to % w/w. [Note—Isopropyl alcohol has a density of 0.79 g/mL, and 70% v/v isopropyl alcohol has a density of 0.85 g/mL. ]
70 mL of isopropyl alcohol × (0.79 g/mL) = 55.3 g of isopropyl alcohol
100 mL of solution × (0.85 g/mL) = 85 g of solution
(55.3 g of isopropyl alcohol/85 g of solution) × 100 = 65.06% w/w
3. Convert 70% v/v isopropyl alcohol to % w/v. The following values are from example 2.
55.3 g of isopropyl alcohol/100 mL of solution = 55.3% w/v
4.Convert 50% w/w glycerin to molality (m). [Note—Glycerin has a MW of 92.1. ]
50 g of glycerin/(92.1 g/mol) = 0.543 mol of glycerin
100 g of solution 50 g of glycerin = 50 g of water = 0.05 kg of water
(0.543 mol of glycerin/0.05 kg of water) = 10.86 m
5.Convert 70% v/v isopropyl alcohol to molality (m). [Note—Isopropyl alcohol has a density of 0.79 g/mL and a MW of 60.1; 70% v/v isopropyl alcohol has a density of 0.85 g/mL. ]
70 mL of isopropyl alcohol × (0.79 g/mL) = 55.3 g of isopropyl alcohol
100 mL of solution × (0.85 g/mL) = 85 g of solution
(85 g of solution 55.3 g of isopropyl alcohol) = 29.7 g of water = 0.0297 kg of water
55.3 g of isopropyl alcohol/(60.1 g/mol) = 0.92 mol of isopropyl alcohol
(0.92 mol of isopropyl alcohol/0.0297 kg of water) = 30.98 m
6.Convert 50% w/w glycerin to molarity (M). [Note—Glycerin has a MW of 92.1 g. ]
From example 1, 50% w/w glycerin = 56.5% w/v glycerin
(56.5 g/100 mL) × (mol/92.1 g) × (1000 mL/L) = 6.13 M
7.Convert 50% w/w glycerin to % v/v. [Note—50% w/w of glycerin has a density of 1.13 g/mL; 100% glycerin has a density of 1.26 g/mL. ]
50 g of glycerin/(1.26 g/mL) = 39.7 mL of glycerin
100 g of solution/(1.13 g/mL) = 88.5 mL of solution
(39.7 mL of glycerin/88.5 mL of solution) × 100% = 44.8% v/v
9.Convert 50% w/w glycerin to 1 in R ratio strength.
1/R = (50 g of glycerin/100 g of solution)
R = 2
1 in R = 1 in 2
8.3.3 solid and semisolid in solid and semisolid mixture conversions
The calculations used to convert from percent weight in weight (% w/w) to ppm and ratio strengths are illustrated as follows for fluocinonide and tolnaftate in topical semisolids and powders.
8.3.3.1 Calculating solid and semisolid in solid and semisolid mixture conversions
Examples—Solid and semisolid in solid and semisolid mixture conversions
1.Convert 0.05% w/w fluocinonide ointment to ppm.
(0.05 g/100 g) × (1 × 106 ppm) = 500 ppm
2.Convert 1.5% w/w tolnaftate powder to 1:R ratio strength.
1/R = (1.5 g of tolnaftate/100 g of powder)
R = 67
1:R = 1:67
3.Convert 1% w/w tolnaftate in talcum powder to X:Y ratio strength.
100 g of powder 1 g of tolnaftate = 99 g of talcum
X:Y = 1 g of tolnaftate:99 g of talcum
8.4 Dilution and Concentration
A more concentrated solution can be diluted to a lower concentration to obtain appropriate strength and precision when compounding preparations. Powders and semisolid mixtures can be triturated or mixed to achieve lower concentrations. The amount of an ingredient in the diluted mixture is the same as that in the portion of the more concentrated source used to make the dilution; thus, the following equation can be applied to dilution problems (Q1)(C1) = (Q2)(C2), where Q1 and Q2 are the quantity of solutions 1 and 2, respectively, and C1 and C2 are concentrations of solutions 1 and 2, respectively. Any quantities and concentration terms may be used but the units of those terms must be the same on both sides of the equation.
8.4.1 calculating dilution and concentration
Examples—Dilutions and fortifications
1. Semisolid dilution
Calculate the quantity (Q2), in g, of diluent that must be added to 60 g of a 10% w/w ointment to make a 5% w/w ointment.
(Q1) = 60 g, (C1) = 10% w/w, and (C2) = 5% w/w
60 g × 10% w/w = (Q2) × 5% w/w
(Q2) = 120 g
120 g 60 g = 60 g of diluent to be added
2.Solid dilution
Calculate the amount of diluent that should be added to 10 g of a trituration (1 in 100) to make a mixture that contains 1 mg of drug in each 10 g of the final mixture.
Convert mg to g: 1 mg of drug = 0.001 g of drug
10 g of mixture should contain 0.001 g of drug
(Q1) = 10 g, (C1) = (1 in 100), and (C2) = (0.001 in 10)
10 g × (1/100) = (Q2) × (0.001/10)
(Q2) = 1000 g
Because the final mixture of 1000 g contains 10 g of the trituration, 990 g (or 1000 g 10 g) of diluent is required to prepare the mixture at a concentration of 0.001 g of drug in each 10 g.
3. Liquid dilution
Calculate the percentage strength (C2) of a solution obtained by diluting 400 mL of a 5.0% w/v solution to 800 mL.
(Q1) = 400 mL, (C1) = 5.0% w/v, and (Q2) = 800 mL
400 mL × 5% w/v = 800 mL × (C2)
(C2) = 2.5% w/v
4. Liquid fortification
Calculate the additional amount, in g, of codeine phosphate that need to be added to 180 mL of a 12 mg/5 mL elixir of acetaminophen with codeine to have a final concentration of 30 mg/5 mL of codeine phosphate.
Amount to add = Total amount required Amount present
Total amount required: (30 mg/5 mL) × 180 mL = 1080 mg of codeine phosphate
Amount present = (12 mg of codeine/5 mL) × 180 mL = 432 mg of codeine phosphate
Amount to add: 1080 mg 432 mg = 648 mg of codeine phosphate

9. ALCOHOL
To achieve compliance with the statements in the General Notices and Requirements about Alcohol and the USP monograph for Alcohol, some conventions and special calculations are needed. See General Notices and Requirements 5.20.20.1 In Compounded Preparations, 8.30 Alcohol Content, and Labeling 7, Alcohol for information. The USP monograph for Alcohol states that it contains 92.3%–93.8% by weight corresponding to 94.9%–96.0% by volume of alcohol (C2H5OH) at 15.56. The percent concentration for alcohol is generally taken to be 95% v/v of alcohol (C2H5OH) in water.
In summary:
  • When the word alcohol is written on a prescription order or in a formula, as for example “alcohol 10 mL” or “dissolve in 5 mL of alcohol”, the compounder should use the Alcohol, USP [that is 95% alcohol (C2H5OH)].
  • When the word alcohol is written with a percent, for example “alcohol 20%”, this means 20% v/v of alcohol (C2H5OH). If this percent is on a label of a commercial product, it means the product contains 20% v/v alcohol (C2H5OH). If this is part of a compounding formula, it means the compounder must add the equivalent of 20% v/v alcohol (C2H5OH), which may require special calculations.
  • Labels of products and compounded preparations are to include the content of alcohol (C2H5OH) in % v/v. For compounded preparations, this value must often be calculated based on the volume(s) of alcohol-containing ingredients added.
For calculations when preparing compounded drug preparations using Alcohol, USP, the first step is to determine the quantity, in mL, of alcohol needed, and the second step is to determine the % v/v of alcohol (C2H5OH) in the final preparation so that it can be properly labeled.
9.1 Calculating Alcohol
Examples—Alcohol
1. Determine the quantity of alcohol needed for the prescription (see Table 3):
Table 3
Clindamycin 1%
Alcohol 15%
Propylene glycol 5%
Purified water, a sufficient quantity to make 60 mL
  1. In this prescription order, the alcohol 15% means the preparation contains 15% v/v of alcohol (C2H5OH).
  2. For 60 mL of preparation, calculate the quantity of alcohol (C2H5OH) needed:
    15% v/v × 60 mL = 9 mL of alcohol
  3. Because the source of alcohol (C2H5OH) is Alcohol, USP, calculate the volume, in mL, of Alcohol, USP needed to give 9 mL of alcohol (C2H5OH):
    9 mL alcohol/95% v/v Alcohol, USP = 9.5 mL of Alcohol, USP
    Therefore, add 9.5 mL of Alcohol, USP to this preparation.
  4. Determine the % v/v alcohol content for labeling.
    Because labeling of alcohol is in % v/v of alcohol (C2H5OH), the alcohol content of this preparation would be labeled: Alcohol 15%.
2. Determine the alcohol content, in % v/v, for the prescription (see Table 4):
Table 4
Castor oil 40 mL
Acacia As needed
Alcohol 15 mL
Cherry syrup 20 mL
Purified water, a sufficient quantity to make 100 mL
Because the USP monograph for Alcohol is to be used when alcohol is called for in formulas, measure 15 mL of Alcohol, USP.
95% Alcohol, USP × 15 mL = 14.25 mL of alcohol
14.25 mL of alcohol/100 mL of preparation = 14.25% alcohol

10. ALLIGATION ALTERNATE AND ALGEBRA METHODS
10.1 Alligation Alternate
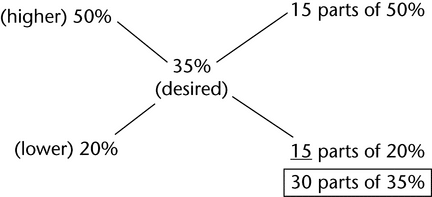
Alligation is a method of determining the proportions in which substances of different strengths are mixed to yield a desired strength or concentration. Once the proportion is found, the calculation may be performed to find the exact amounts of substances required.
Set up the problem as follows.
  1. Place the desired percentage or concentration in the center.
  2. Place the percentage of the substance with the lower strength on the lower left-hand side.
  3. Place the percentage of the substance with the higher strength on the upper left-hand side.
  4. Subtract the lower percentage from the desired percentage, and place the obtained difference on the upper right-hand side.
  5. Subtract the desired percentage from the higher percentage, and place the obtained difference on the lower right-hand side.
The results on the right side determine how many parts of the two different percentage strengths should be mixed to produce the desired percentage strength of a drug mixture. The total parts will equal the final weight or volume of the preparation.
10.1.1 calculating by using the alligation alternate
Examples—Alligation alternate
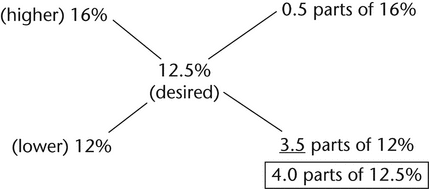
1.Determine the amount of ointment containing 12% drug concentration and the amount of ointment containing 16% drug concentration must be used to make 1 kg of a preparation containing a 12.5% drug concentration.
Click to View Image
In a total of 4 parts of 12.5% preparation, 3.5 parts of 12% ointment and 0.5 parts of 16% ointment are needed.
4 parts correspond to 1 kg or 1000 g.
1 part corresponds to 250 g.
3.5 parts correspond to 3.5 × 250 g or 875 g of 12% ointment.
0.5 parts correspond to 0.5 × 250 g or 125 g of 16% ointment.
2. Determine the volume, in mL, of 20% dextrose in water and 50% dextrose in water needed to make 750 mL of 35% dextrose in water.
Click to View Image
In a total of 30 parts of 35% dextrose in water, 15 parts of 50% dextrose in water and 15 parts of 20% dextrose in water are required.
30 parts correspond to 750 mL.
15 parts correspond to 375 mL.
Thus, use 375 mL of the 20% solution and 375 mL of the 50% solution to prepare the preparation.
10.2 Algebra Method
The following algebraic equation may be used instead of alligation to solve problems of mixing two different strengths of the same ingredient:
(Cs × Qs) + (Cw × Qw) = (Cf × Qf), where C is concentration or strength, Q is the quantity; and the subscript s identifies the strongest strength, w identifies the weakest strength, f represents the final mixture with a strength less than s and greater than w, (Qs + Qw) = Qf, Qs = (Qf Qw), and Qw = (Qf Qs).
10.2.1 calculating by using the algebra method
Examples—Algebra method
1. Determine the amount, in g, of 16% w/w drug ointment and 12% w/w drug ointment required to prepare 1 kg of 12.5% w/w drug ointment.
(16% × Qs) + [12% × (1000 g Qs)] = 12.5% × 1000 g
16% Qs + 120 g 12% Qs = 125 g
4% Qs = 5 g
Qs = 5 g/4% = 125 g of 16% ointment
Qw = 1000 g 125 g = 875 g of 12% ointment
2. Determine the volume, in mL, of 10% dextrose injection and 50% dextrose injection needed to make 750 mL of 35% dextrose injection.
(50% × Cs) + [10% × (750 mL Cs)] = 35% × 750 mL
50% Cs + 75 mL 10% Cs = 262.5 mL
40% Cs = 187.5 mL
Cs = 187.5 mL/40% = 468.75 mL (470 mL practically)
Cw = 750 mL 468.75 mL = 281.25 mL (280 mL practically)

11. ALIQUOT CALCULATIONS
When the quantity of drug desired requires a degree of precision in measurement that is beyond the capability of the available measuring devices, the pharmacist may use the aliquot method of measurement. It applies when potent drug substances are compounded, or when the total amount of the active drug in a single dose or individualized doses is less than the minimum accurately weighable quantity (MAWQ). Even if the amount of drug needed is greater than the MAWQ per unit, an aliquot will provide more material per unit, which will aid in handling and administration. Aliquot means “containing an exact number of times in something else”; the aliquot must be a proportional part of the total. Therefore, 5 is an aliquot part of 15, because 5 is contained exactly 3 times in 15. Both the total volume of solution or weight of powder triturate and the aliquot volume/weight should be easily and accurately measurable. If the solution or powder triturate is highly concentrated and a small error is made in measuring the aliquot, a large error can occur in the quantity of drug brought to the final formulation.
Aliquots can be: solid–solid, when the active drug and the diluents are solids; solid–liquids, when the active drug is solid and is to be incorporated into a liquid preparation, such as a solution, an emulsion, or a suspension; and liquid–liquid, when the active drug is liquid and the diluents are liquids. It can be a pure liquid or a concentrated solution of a drug. Aliquots of pure liquids are relatively uncommon because few drugs are liquid in their pure state. Aliquots involving concentrated solutions are more common.
There are two general methods to prepare aliquots:
  1. Aliquot method 1 is applicable to drugs or substances that have to be within the degree of accuracy provided by the measuring device. It is the simplest method and can be applied to solid and liquid aliquots.
  2. Aliquot method 2, also known as the dilution factor method, is useful when there is more flexibility in the amount of drug that may be measured.
Aliquot Method 1:
  1. The MAWQ amount of drug is measured.
  2. The drug is diluted with an arbitrary amount of diluent.
  3. The amount of dilution that will give the desired amount of drug is calculated, and the amount is measured.
Aliquot Method 2:
  1. The quantity of drug to be measured is determined by multiplying the amount of drug needed by an appropriately determined factor, called the dilution factor. The dilution factor must be a whole number more than or equal to the MAWQ divided by the amount of drug needed.
  2. An arbitrary amount of diluent is measured and added. The amount of diluent used can be determined by different methods, provided the amount of diluent chosen will give an aliquot greater than or equal to the MAWQ.
  3. The amount of aliquot needed is determined by multiplying the weight or volume of the dilution by the inverse of the dilution factor. Dilution factors are usually chosen to be whole numbers.
The general calculations can be shown as:
A/B = C/D

A= amount of drug desired
B= amount of drug measured
C= amount of drug in aliquot
D= aliquot total amount
11.1 Calculating Aliquots
Examples—Aliquots
1. Solid-in-liquid dilution (Aliquot Method 1)
Prepare 100 mL of a solution containing 0.2 mg/mL of clonidine using water as the diluent. To prepare this solution, 20 mg of clonidine is needed.
  1. Select the weight of drug desired (A) to be equal to or greater than the MAWQ. In this situation, the MAWQ of the balance is 120 mg.
  2. Select the aliquot volume (D) in which the desired amount of drug (C) will be contained. This establishes the concentration of the solution to be prepared. Clonidine solubility is 1 g/13 mL, so if 5 mL is selected as the aliquot volume, the concentration in that solution will be 20 mg/5 mL. Therefore, solubility will not be a problem in this aqueous solution.
  3. Using the preceding formula, calculate the volume of solution (B) to be prepared.
    120 mg of clonidine/B = 20 mg of clonidine/5 mL of aliquot
    B = 30 mL
  4. Prepare the solution containing 120 mg of clonidine in 30 mL of Purified Water. Transfer a 5-mL aliquot from this solution to a final container, and add sufficient Purified Water to bring the formulation to a final volume of 100 mL.
2. Solid-in-solid dilution (Aliquot Method 2)
Prepare an individual dose of codeine phosphate 20 mg.
  1. Select a dilution factor that will yield a quantity that is greater than or equal to the MAWQ, and weigh this amount. In this case, the dilution factor may be greater than or equal to 6 because 6 × 20 mg = 120 mg. The smallest dilution factor that may be chosen is 6 if the MAWQ of the balance is 120 mg.
  2. Weigh an amount of diluent that will give an aliquot greater than or equal to the MAWQ. In this example, 600 mg of diluent is weighed.
  3. Mix the two powders thoroughly by geometric trituration in a mortar.
  4. Calculate the total weight of the dilution: 120 mg codeine phosphate + 600 mg diluent = 720 mg.
  5. Calculate the aliquot part of the dilution that contains 20 mg of codeine phosphate by multiplying the total weight of the dilution by the inverse of the dilution factor: 720 mg × (1/6) = 120 mg.
  6. Weigh this calculated amount of the dilution (120 mg) to get the desired 20 mg of codeine phosphate per dose.

12. POWDER VOLUME CALCULATIONS
12.1 Displacement in Suspension
12.1.1 calculating powder volume
Examples—Powder volume
1. Powder displacement in suspension
The directions to reconstitute a 150 mL bottle of an amoxicillin for oral suspension of 250 mg/5 mL require 111 mL of Purified Water. The physician has requested that the product be reconstituted at a concentration of 500 mg/5 mL. Calculate the amount of Purified Water required for the higher concentration.
  1. Calculate the volume of the suspension occupied by the amoxicillin powder:
    150 mL 111 mL = 39 mL
  2. Calculate the quantity of amoxicillin present in the entire bottle:
    150 mL × (250 mg/5 mL) = 7500 mg
  3. Calculate the total volume of the suspension at the requested concentration (500 mg/5 mL):
    7500 mg/(500 mg/5 mL) = 75 mL
  4. Calculate the volume of Purified Water needed to reconstitute the powder by subtracting the powder volume calculated in step a:
    75 mL 39 mL = 36 mL of Purified Water
Note—Such formulations may be too viscous to flow freely.
2.Powder volume in drugs for injection
If the powder volume of 250 mg of ceftriaxone for injection is 0.1 mL, calculate the amount of diluent that should be added to 500 mg of ceftriaxone for injection to make a suspension with a concentration of 250 mg/mL.
  1. Calculate the total volume of injection:
    500 mg/(250 mg/mL) = 2 mL
  2. Calculate the volume occupied by 500 mg of ceftriaxone for injection:
    500 mg/(250 mg/0.1 mL) = 0.2 mL
  3. Calculate the volume of the diluent required:
    (2 mL of suspension) (0.2 mL of ceftriaxone for injection) = 1.8 mL of diluent

13. INTRAVENOUS FLOW OR INFUSION RATES
Intravenous (IV) solutions and emulsions may be administered by gravity flow and infusion or syringe pumps. Gravity-flow IV sets are regulated by an adjustable clamp on the tubing, and the approximate flow rate is determined by counting the number of drops per 10–15 seconds, then adjusting that to a per minute rate. Manufactured IV sets are typically calibrated to deliver from 15 to 60 drops/mL, depending on the particular set.
13.1 Solving by Multiple or Separate Steps
As in previous sections, the following examples may be solved by multiple separate steps, or a single-DUA procedure.
13.1.1 calculating intravenous flow or infusion rates
Examples—IV or infusion rates
1.An IV infusion of dextrose 5% in water with 20 mEq of potassium chloride is to be administered to a 6-year-old child at the rate of 12 mL/hour. An IV administration set that delivers 60 drops/mL is available. Calculate the flow rate in drops/minute:
Click to View Image
2.A 63.6-kg patient is admitted to the Emergency Department and requires a dopamine hydrochloride infusion to maintain an adequate blood pressure. The drug is ordered at an initial rate of 2 µg/kg/minute. A 400-mg/250-mL dopamine hydrochloride injection is available. Calculate the flow rate in mL/hour to be administered by infusion pump:
Click to View Image

14. ISOOSMOTIC SOLUTIONS
The following discussion and calculations have therapeutic implications in preparations of dosage forms intended for ophthalmic, subcutaneous, intravenous, and intrathecal administration as well as for neonatal use.
14.1 Tonicity
Cells of the body, such as erythrocytes, will neither swell nor shrink when placed in a solution that is isotonic with body fluids. The measurement of tonicity, however, which is a physiological property, is somewhat difficult. A 0.9% w/v sodium chloride injection, which has a freezing point (FP) of 0.52, is both isotonic and isoosmotic with body fluids. In contrast to isotonicity, FP depression is a physical property. Some solutions that are isoosmotic with body fluids are not isotonic, because they contain solutes to which cells are freely permeable rather than semipermeable. Freely permeable solutes (e.g., boric acid and urea) can cause erythrocyte lysis, i.e., behave as if they were hypotonic in concentrations that are hyperosmotic relative to body fluids. Nevertheless, many pharmaceutical products are prepared using FP data or related sodium chloride data to prepare solutions that are isoosmotic with body fluids. A closely related topic is osmolarity (see chapter Osmolality and Osmolarity 785).
FP data or sodium chloride equivalents of pharmaceuticals and excipients (see Table 5) may be used to prepare isoosmotic solutions, as shown in the following examples.
14.1.1 calculating tonicity
Example—Tonicity
Determine the amount of sodium chloride (NaCl) required to prepare 60 mL of an isoosmotic solution of atropine sulfate injection 0.5% using the E values and the FP depression values in Table 5.
Table 5. Sodium Chloride Equivalents (E) and FP Depressions for a 1% Solution of the Drug or Excipient
Drug or Excipient E FP Depression
Atropine sulfate 0.13 0.075
Sodium chloride 1.00 0.576
Using the E values:
  1. The total amount of substances equivalent to a 0.9% sodium chloride injection = (0.9 g/100 mL) × 60 mL = 0.54 g.
  2. The amount of atropine sulfate required = (0.5 g/100 mL) × 60 mL = 0.3 g.
  3. 1 g of atropine sulfate is equivalent to 0.13 g of sodium chloride.
  4. 0.3 g of atropine sulfate is equivalent to 0.3 × 0.13 g = 0.039 g of sodium chloride.
  5. Thus, the required amount of sodium chloride is 0.54 g 0.039 g = 0.501 g or 0.5 g.
Using FP depression values:
  1. The FP depression required is 0.52.
  2. A 1% solution of atropine sulfate causes an FP depression of 0.075.
  3. A 0.5% solution of atropine sulfate causes an FP depression of 0.5 × 0.075 = 0.0375.
  4. The additional FP depression required is 0.52 0.0375 = 0.483.
  5. A 1% solution of sodium chloride causes an FP depression of 0.576.
  6. Therefore, an FP depression of 1 is caused by a 1%/0.576 = 1.736% solution of sodium chloride.
  7. 1.736% × 0.483 = 0.838% solution of sodium chloride causes an FP depression of 0.482.
  8. The required amount of sodium chloride is (0.838%) × 60 mL = 0.502 g or 0.5 g.

15. pH AND BUFFER CALCULATIONS
15.1 pH Calculations
See Appendix 1 for logarithmic definitions and applications.
pH = log [H3O+], and pKa = log ([H3O+][A–])/[HA], where [H3O+] is the hydrodium ion concentration in an aqueous solution, [A–] is the ionic form of the relevant acid, and Ka is the ionization constant of either a monoprotic acid or a particular proton from a polyprotic acid in aqueous solution. The [H+] = the antilogarithm of (pH) or 10pH; and Ka = the antilogarithm of (pKa) or 10pKa.
The pH of an aqueous solution containing a weak acid may be calculated using the Henderson–Hasselbalch equation:
pH = pKa + log [(base form)/(acid form)]
The buffer equation symbol () represents the equilibrium between conjugate base and acid forms or pairs of the same molecule. It is called the buffer equation, because small changes in the ratio of concentrations of the conjugate forms result in a logarithmically smaller change in pH. The salt form can be an acid or base, depending on structure; thus, its conjugate form is a base or acid, respectively.
Example 1:
B and BH+ represent a nonionized or “free” base and cationic acid pair, BH+ B+H+
Example 2:
HA and A– represent a nonionized or “free” acid and anionic base pair, HA A– + H+
Example 3:
HnA– and Hn1A2, such as H2PO4– and HPO42, represent an anionic acid and anionic base relative to each other; the pKa = 7.2 for H2PO4– HPO42 + H+.
15.1.1 calculating ph
Example—pH
A solution contains 0.020 mol/L of sodium acetate and 0.010 mol/L of acetic acid, which has a pKa value of 4.76. Calculate the pH and the [H+] of the solution as follows:
pH = 4.76 + log (0.020/0.010) = 5.06
[H+] = antilogarithm of (5.06) = 8.69 × 106
15.2 Buffer Solutions
15.2.1 definition
A buffer solution is an aqueous solution that resists a change in pH when small quantities of acid or base are added, when diluted with the solvent, or when the temperature changes. Most buffer solutions are mixtures of a weak acid and one of its salts, or mixtures of a weak base and one of its salts. Water and solutions of a neutral salt, such as sodium chloride, have very little ability to resist the change of pH and are not capable of effective buffer action.
15.2.2 preparation, use, and storage of buffer solutions
Buffer solutions for Pharmacopeial tests should be prepared using freshly boiled and cooled water (see Reagents, Indicators and Solutions). They should be stored in containers such as Type I glass bottles and used within 3 months of preparation.
Buffers used in physiological systems are carefully chosen so as to not interfere with the pharmacological activity of the medicament or the normal function of the organism. Commonly used buffers in parenteral products, for example, include: the nonionized acid and base salt pairs of acetic acid and sodium acetate, citric acid and sodium citrate, glutamic acid and sodium glutamate, and monopotassium or monosodium phosphate and dipotassium or disodium phosphate; and the acid salt and nonionized base pair tris(hydroxymethyl)aminomethane hydrochloride and tris(hydroxymethyl)aminomethane. Buffer solutions should be freshly prepared.
The Henderson–Hasselbalch equation, noted in 15.1 pH Calculations, allows calculation of the pH and concentrations of conjugate pairs of weak acids and their salts and weak bases and their salts in buffer solutions when the pKa of the acid form of the buffer pair is known. Appropriately modified, this equation may be applied to buffer solutions composed of a weak base and its salt.
15.2.3 buffer capacity
The buffer capacity of a solution is the measurement of the ability of that solution to resist a change in pH upon addition of small quantities of a strong acid or base. An aqueous solution has a buffer capacity of 1 when 1 L of the buffer solution requires 1 g equivalent of strong acid or base to change the pH by 1 unit. Therefore, the smaller the pH change upon the addition of a specified amount of acid or base, the greater the buffer capacity of the buffer solution. Usually, in analysis, much smaller volumes of buffer are used to determine the buffer capacity. An approximate formula for calculating the buffer capacity is g equivalents of strong acid or base added per L of buffer solution per unit of pH change, i.e., (g equivalents/L)/(pH change).
15.2.4 calculating buffer capacity
Example—Buffer capacity
The addition of 0.01 g equivalents of sodium hydroxide to 0.25 L of a buffer solution produced a pH change of 0.50. The buffer capacity of the buffer solution is calculated as follows:
(0.01 Eq/0.25 L)/0.50 pH change = 0.08(Eq/L)/(pH change)

16. TEMPERATURE
The relationship between Celsius or Centigrade (C) and Fahrenheit (F) temperature scale is expressed by the following equations:
C = (F 32) × (5/9)
F = (C × 1.8) + 32
16.1 USP Temperatures
According to the General Notices and Requirements 8.180 Temperatures, temperatures are expressed in centigrade (Celsius) degrees, and all other measurements are made at 25 unless otherwise indicated. For instructional purposes, F is shown in the examples.
16.1.1 calculating temperatures
Examples—Temperatures
1.Convert 77F to Celsius degrees.
C = (77F 32) × (5/9) = 25C
2.Convert 30C to Fahrenheit degrees.
F = (30C × 1.8) + 32 = 86F
The relationship between the Kelvin or absolute (K) and the Celsius (C) scales is expressed by the equation:
K = C + 273.1

17. ENDOTOXINS
An endotoxin is a lipopolysaccharide that comes from a particular source, where species and strain number are usually indicated.
17.1 Endotoxin Concentrations
For more information concerning endotoxins, see Bacterial Endotoxins Test 85.
17.1.1 calculating endotoxins
Example—Endotoxins
A 71.8-kg patient is to receive an intrathecal infusion of morphine sulfate at a rate of 0.3 mg/hour. The solution will be prepared by diluting preservative-free morphine sulfate injection, which contains 10 mg/mL of morphine sulfate, with 0.9% sodium chloride injection to produce an infusion rate of 2 mL/h.
  1. Determine the volume, in mL, of morphine sulfate injection (10 mg/mL) and 0.9% sodium chloride injection needed to prepare a 24-hour infusion.
    0.3 mg of morphine sulfate/hour × 24 hours = 7.2 mg of morphine sulfate
    7.2 mg of morphine sulfate/(10 mg/mL) = 0.72 mL of morphine sulfate injection
    2 mL of infusion/h × 24 h = 48 mL of total volume
    48 mL total volume 0.72 mL morphine sulfate injection = 47.28 mL of 0.9% sodium chloride injection
  2. Calculate the maximum potential endotoxin load/hour for this preparation. [Note—USP monographs specify upper limits of 14.29 USP Endotoxin Units (EU)/mg of morphine sulfate in injections for intrathecal use, and 0.5 EU/mL for injections containing 0.5%–0.9% sodium chloride. ]
    7.2 mg of morphine sulfate injection × 14.29 EU/mg of morphine sulfate = 102.89 EU from morphine sulfate
    47.28 mL of sodium chloride injection × 0.5 EU/mL = 23.64 EU from 0.9% sodium chloride injection
    Endotoxin load = 102.89 EU + 23.64 EU = 126.53 EU
    126.53 EU/24 hour = 5.27 EU/hour
  3. Determine if the endotoxin load in step 2 exceeds the allowable USP limit for this patient. [Note—The maximum endotoxin load by intrathecal administration is 0.2 EU/kg/hour (see chapter 85). ]
    Maximum endotoxin load = (0.2 EU/kg/hour) × 71.8 kg-patient = 14.36 EU/hour
    The endotoxin load of 5.27 EU/hour does not exceed the allowable limit of 14.36 EU/hour.

18. STABILITY AND EXPIRATION DATE CALCULATIONS
18.1 Stability Based on Rate Calculations
Calculation of a predetermined minimum percentage of initial drug strength or other quality parameter, e.g., in vitro dissolution of active pharmaceutical ingredients (APIs) or active drugs in solid oral dosage forms, is based on component-specific assays and other validated scientific testing. The expiration date or time elapsed until such minimum acceptable limits are reached for a specific manufactured product is exclusive to the specific formulation, packaging, and environmental conditions, e.g., temperature, humidity, and illumination, to which the item is subjected. See also chapters 659, 795, 797, 1163, and 1191.
The degradation or concentration loss rates or kinetics of most APIs can be accurately represented or modeled by either zero order (constant) or first order (mono-exponential) rate equations. Zero order calculations are generally applicable to solids, semisolids, suspensions in which a majority of the drug strength is present as solid particles, and auto-oxidation in solutions. First order calculations are generally applicable for drug hydrolysis in solutions.
18.2 Zero Order Rate Calculations
The isothermal zero order or constant rate equation for a particular formulation is C = C0 kt, where C is the concentration of API at any time, C0 is the concentration at origination or time zero, k is the reaction rate constant, and t is any time after origination or zero. The values and units of the rate, dC/dt, and rate constant, k, are the same for zero order processes, i.e., the units are concentration/time, such as mg/mL/day.
18.2.1 zero order rate equation derived from original data
The following examples illustrate calculations of the zero order rate equation from original concentration assay and time data, and an expiration date using that equation.
18.2.1.1 Calculating zero order rate
Examples—Zero order rate
1.Calculate the zero order rate equation based on the assay results for a drug suspension at 25 (see Table 6):
Table 6
C (mg/mL) t (days)
49 3
47.5 8
44.8 17
42.3 26
Linear regression of the C (ordinate) versus t (abscissa) values yields the equation, C = 49.84 0.292t with a correlation coefficient of 0.9996.
2. Calculate the time when C = 0.9 × C0, i.e., the expiration date where the concentration will be 90% of the original concentration (t90):
C = 49.84 0.292t
0.9 × 49.84 = 49.84 0.292(t90)
t90 = (44.86 49.84)/0.292 = 17.05 days
3.Using the previous linear regression equation, calculate the C of the drug suspension at 25 when t = 12 days:
C = 49.84 (0.292 × 12) = 46.34 mg/mL
4. Calculate t when C = 45 mg/mL:
45 = 49.84 0.292t
t = (45 49.84)/0.292 = 16.6 days
18.2.2 zero order values calculated from a rate equation
The following are examples of expiration dates calculated from a rate equation derived from original concentration assay and time data.
18.2.2.1 Calculating zero order values from a rate equation
Examples—Zero order from a rate equation
1. Calculate the t80 expiration date of a drug cream at 25 using the equation, C = 0.05 0.0003t, where the C unit is % w/w and the t unit is months. At t80, C = 0.8C0.
0.8 × 0.05 = 0.05 0.0003(t80)
t80 = 33.3 months
2. Calculate the t80 expiration date of the drug cream formulation in example 1, but for which C0 is 0.1:
0.8 × 0.1 = 0.1 0.0003(t80)
t80 = 66.7 months
18.3 First Order Rate Calculations
The isothermal first order rate equation for a particular formulation in exponential form is C = C0ekt, and in linear form is ln(C) = ln(C0)kt, where C is the concentration of an API at any time, C0 is the concentration at origination or time zero, k is the reaction rate constant, and t is any time after origination or zero. The constantly changing rate, dC/dt, and rate constant, k, are not the same for first order processes. The rate units are concentration/time, e.g., mg/mL/hour, but the rate constant unit is reciprocal time, time1, e.g., hour1.
18.3.1 first order linear rate equation derived from original data
The following examples illustrate calculation of the linear first order rate equation from original concentration assay and time data and calculation of an expiration date using that equation.
18.3.1.1 Calculating first order linear rate equations
Example—First order linear rate
1. Calculate the linear first order rate equation based on the assay results for a drug solution at 27 (see Table 7):
Table 7
C (mg/mL) t (hour)
12.3 2
11.9 6
11.5 14
10.6 24
Linear regression of the ln(C) (ordinate) versus t (abscissa) values yields the equation, ln(C) = 2.522 0.0065t with a correlation coefficient of 0.992.
2. From the linear regression equation, calculate the time when 95% of the original concentration is reached, t95, when C = 0.95C0, which is the predetermined expiration date:
ln(C0) = 2.522; thus, C0 = e2.522 = 12.45 mg/mL
ln(0.95 × 12.45) = 2.522 0.0065(t95)
t95 = (2.470 2.522)/0.0065 = 8 hours
18.3.2 first order values calculated from a linear equation
The following are examples of an expiration date, concentration, and time calculated for the same drug solution at 22 from the rate equation, ln(C) = 4.382 0.076t, where the C units are µg/mL and the t unit is days, derived from the original concentration assay and time data.
18.3.2.1 Calculating first order values from a linear rate equation
Examples—First order from a linear rate
1.Calculate the t90 expiration date:
ln(C0) = 4.382; thus, C0 = e4.382 = 80
ln(0.9 × 80) = 4.382 0.076(t90)
t90 = (4.277 4.382)/0.076 = 1.4 days
2.Calculate the time at which C = 75 µg/mL:
ln(75) = 4.382 0.076t
t = (4.317 4.382)/0.076 = 0.86 day
3.Calculate whether C = 70 µg/mL occurs before or after t90:
ln(70) = 4.382 0.076t
t = (4.248 4.382)/0.076 = 1.8 days
C = 70 µg/mL occurs at 1.8 days, after a t90 of 1.4 days
18.3.3 first order expiration date calculated from two values of concentration and time
When degradation or other cause of concentration loss is known from experience or reference information to obey first order kinetics, the rate constant can be accurately estimated from accurate assays of only two concentrations at their respective times. In this case, the linear first order rate equation, ln(C) = ln(C0) kt, may be transformed or integrated as ln(C2) = ln(C1) k(t2 t1), which when rearranged is k = ln(C1/C2)/(t2 t1). The following examples apply these equations to calculate expiration dates, concentrations, and times.
18.3.3.1 Calculating first order expiration date from two values
Examples—First order expiration date from two values
1.At 25, the concentration of an antibiotic in solution was 89 mg/mL after 3 hours and 74 mg/mL after 8 hours. Calculate the initial concentration at time zero:
k = ln(89/74)/(8 3) = 0.037 hour1
ln(89) = ln(C0) (0.037 hour1 × 3 hour)
ln(C0) = 4.489 + 0.111 = 4.6
C0 = e4.6 = 99.5 mg/mL
2.Calculate the t90 expiration date using the data in example 1. At t90, C = 0.9C0.
ln(0.9 × 99.5) = ln(99.5) 0.037(t90)
t90 = (4.495 4.600)/0.037 hour1 = 2.8 hour
3.Calculate the concentration at 6 hour using the data in example 1:
ln(C) = ln(99.5) (0.037 × 6)
ln(C) = 4.378
C = e4.378 = 79.7 mg/mL
18.3.4 first order times, tn, for 0.n fraction or n% of remaining original concentration
The two most common first order pharmaceutical tn values are the t50, which is a primary parameter factor in clinical pharmacokinetics, and the t90, which is the most common stability shelf life or expiration date. Values of any tn, where 0 < n < 100, are derived from the linear first order equation, ln(C) = ln(C0) kt. The equations for t50 and t90 in particular are derived in the following examples. The value of k by definition is constant for a specific drug chemical in a specific formulation at a specific temperature; thus, tn values derived from such values of k are also constant.
18.3.4.1 Calculating first order times for remaining original concentrations
Examples—First order times for remaining original concentrations
1.At tn, C = 0.n × C0.
ln(0.n × C0) = ln(C0) ktn
tn = [ln(0.n × C0) ln(C0)]/k = ln[(0.n × C0)/C0]/k = ln(0.n)/k
tn = ln(0.n)/k
2.At t50, C = 0.5(C0).
ln(0.5 × C0) = ln(C0) kt50
t50 = [ln(0.5 × C0) ln(C0)]/k = ln[(0.5 × C0)/C0]/k = ln(0.5)/k = 0.693/k = 0.693/k
t50 = 0.693/k
3.At t90, C = 0.9(C0).
ln(0.9 × C0) = ln(C0) kt90
t90 = [ln(0.9 × C0) ln(C0)]/k = ln[(0.9 × C0)/C0]/k = ln(0.9)/k = 0.105/k = 0.105/k
t90 = 0.105/k
18.4 Stability Prediction Based on Arrhenius Theory
The basis of the Arrhenius theory is that reaction rates and rate constants change exponentially in the direction of arithmetic temperature change. The pharmaceutical application of the Arrhenius theory is based on scientifically accurate and statistically valid assay data obtained at three or more temperatures that are 10 warmer than the intended drug storage temperature and each other. The Arrhenius equation may be expressed in an exponential form, k = Ae(Ea/RT), a linear form, ln(k) = ln(A) (Ea/RT), and an integrated form, ln(k2/k1) = Ea(T2 T1)/[R(T2 × T1)], where k, k1, and k2 are isothermal rate constants, A is a thermodynamic factor, Ea is energy of activation for the degradation reaction, R is the gas constant (1.987 × 103 kcal mol1K 1 or 8.314 × 103 J K1 mol1), and T, T1, and T2 are absolute or Kelvin temperatures.
18.4.1 arrhenius linear equation derived from original data
The following examples illustrate derivation of a linear Arrhenius equation from original assay data and its application to predicting a drug stability expiration date at a cooler or lower storage temperature.
18.4.1.1 Calculating Arrhenius equations
Examples—Arrhenius equations
1.Calculate the linear Arrhenius equation based on the rate constants and temperatures for a beta-lactam antibiotic that decomposes in solution at a first order rate (see Table 8):
Table 8
T (C) T (K) 1/T (K1) k (hour1) ln(k)
40 313 3.195 × 103 0.0014 6.571
50 323 3.096 × 103 0.005 5.298
60 333 3.003 × 103 0.016 4.135
Linear regression of the ln(k) (ordinate) versus 1/T (abscissa) values yields the equation, ln(k) = 33.977 (12,689/T) with a correlation coefficient of 0.99997.
2.Calculate the t90 shelf life expiration date, in days, at 25C (298 K) using the equation in example 1:
ln(k25) = 33.977 (12,689/298) = 33.977 42.581 = 8.604
k25 = e8.604 = 1.834 × 104 hour1 = 4.402 × 103 day1
t90 = 0.105/k = 0.105/4.402 × 103 day1 = 23.85 days
t90 at 25C = 23.85 days
18.4.2 stability predictions using the integrated arrhenius equation
The following examples illustrate stability predictions based on one accurately determined isothermal rate constant and adherence to the same degradation rate order, e.g., first order, at temperatures at which stability is to be calculated from the equation, ln(k2/k1) = Ea(T2 T1)/[R(T2 × T1)].
18.4.2.1 Calculating stability prediction using integrated Arrhenius equation
Example—Stability using integrated Arrhenius equations
1.Calculate the t85 stability expiration date at 4C (277 K) for an ester hydrolysis with an Ea = 15 kcal/mol and k = 0.0045 hour1 at 23C (296 K):
ln(k277/0.0045) = 15(277 296)/[1.987 × 103 (277 × 296)]
ln(k277) ln(0.0045) = 285/162.92
ln(k277) = 1.749 + ln(0.0045) = 7.153
k277 = e7.153 = 7.825 × 104 hour1
t85 = ln(0.850)/k277 = 0.163/7.825 × 104 hour1 = 208.3 hours
t85 at 4C = 208.3 hours (t85 at 23C is 36.2 hours)
18.4.3 arrhenius-based Q10 stability estimation
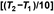The temperature coefficient (Q10) represents the multiplicative factor by which a chemical reaction rate constant changes in the same direction as the temperature for each 10C change. For drug molecules, Q10 ranges from 2 to 5, corresponding to an Ea range of 10–25 kcal/mol or 42–105 kJ/mol. 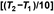A Q10 of 3 yields reasonable estimates of drug stability in the equation, (tn at T2) = (tn at T1)/{Q10Click to View Image}, where n is a percentage of remaining C0, T1 is the temperature at which tn is known, and T2 is the temperature at which tn is to be estimated. Calculations using Q10 values of both 2 and 4 may be used to obtain the shortest or most conservative stability estimate, but Q10 = 3 is applied in the following two examples.
18.4.3.1 Calculating Arrhenius-based Q10 stability estimation
Example—Arrhenius-based Q10 stability
1.Estimate the t90 expiration date in hours of an antibiotic suspension stored in a closed automobile at 57 for which the 8 refrigeration t90 is 14 days.
t90 at 57 = [14 days × (24 hours/day)]/{3[(57 8)/10]} = 336 hours/34.9 = 336 hours/217.7 = 1.54 hours
t90 at 57 = 1.54 hours

Appendix 1: Logarithms
The logarithm of a number is the exponent or power to which a given base number must be raised to equal that number. Thus, the logarithm of Y to the base, b, equals X, or logb(Y) = X. The logarithm of 0 and all negative numbers is undefined or nonexistent. The logarithm of 1 is 0 and of numbers <1 is negative in all systems (see Table 9).
Table 9. Common (or Briggsian) and Natural (or Napierian) Logarithms
Logarithmic System Abbreviation or Symbol Base Number Format Antilogarithm
or Inverse
Logarithm
Common Log 10 log Y = X 10X = Y
Natural Ln e or 2.7183a ln Y = X eX = Y
a   e is an irrational number derived from an infinite series of reciprocal whole number factorials, e = 1 + 1/1! + 1/2! + 1/3! + 1/4! ... + 1/n!, where n = infinity. e rounds to 2.7183 when n 8.
2. The relationships between common and natural logarithms are the following:
  1. log Y = ln Y/ln 10 = ln Y/2.303
  2. ln Y = ln 10 × log Y = 2.303 × log Y
3. Rules for some common calculations with logarithms are shown in Table 10.
Table 10. Rules for Calculating with Logarithms
  Formula Example
Additions and multiplications ln(A) + ln(B) = ln(A × B)
log(A) + log(B) = log(A × B)		 ln(0.62) + ln(1.73) = ln(0.62 × 1.73) = ln(1.0726) = 0.070
log(5.7) + log(0.43) = log (5.7 × 0.43) = log(2.451) = 0.389
Subtraction and quotients ln(A) ln(B) = ln(A/B)
log(A) log(B) = log(A/B)		 ln(0.5) ln(4) = ln(0.5/4) = ln(0.125) = 2.079
log(1.57) log(2.48) = log(1.57/2.48) = log(0.6330645) = 0.199
Simple non-base exponentials ln(Yz) = Z × ln(Y)
log(Yz) = Z × log(Y)		 13.6Z = 1.25
ln(1.25) = Z × ln(13.6)
Z = ln(1.25)/ln(13.6) = 0.223/2.610 = 0.085
0.57Z = 2.3
log(2.3) = Z × log(0.57)
Z = log(2.3)/log(0.57) = 0.362/0.244 = 1.484
Base exponentials In (a × e±b) = ln(x) ln(a) ± b = ln(x)

log (a × 10±b) = log(x) log(a) ± b = log(x)		 67 × 10b = 15.1
log(67) + b = log(15.1)
1.826 + b = 1.179
b = 1.179 1.826 = 0.647
1S (USP38)
Auxiliary Information— Please check for your question in the FAQs before contacting USP.
Topic/Question Contact Expert Committee
General Chapter Jeanne H. Sun, Pharm.D.
Associate Scientific Liaison
(301) 230-3361		 (CMP2010) Compounding
USP38–NF33 Page 1303
USP38–NF33 Supplement : No. 1 Page 7141
Pharmacopeial Forum: Volume No. 40(3)